Cap. 7 - Iteraciones
Las computadoras se usan con frecuencia para automatizar tareas repetitivas. Repetir tareas idénticas o similares sin cometer errores es algo que las computadoras hacen bien y las personas no tanto.
La ejecución repetida de un conjunto de sentencias se llama iteración. Es tan común, que Python provee muchas opciones para implementarlas con facilidad. Ya vimos la sentencia for en el capítulo 3. Es la forma de iteración que seguramente usarás con más frecuencia. Pero en este capítulo veremos la sentencia while - otra forma de hacer que tu programa realice iteraciones, que es útil en situaciones ligeramente distintas.
Antes de verlo, repasemos algunos puntos...
7.1) Asignación
Como mencionamos antes, es legal hacer más de una asignación a una variable. La nueva asignación hace que la variable existente se asocie a un nuevo valor (y deje de referirse a su valor antiguo).
Por ejemplo, el programa:
tiempo_restante = 15 print(tiempo_restante) tiempo_restante = 7 print(tiempo_restante)
Tendrá como output:
15 7
Porque en la primera llamada a print la variable airtime_remaining vale 15, pero en la segunda vale 7.
Es especialmente importante distinguir entre una sentencia de asignación y una expresión booleana que chequea si se da una igualdad. Dado que Python usa el token igual (=) para la asignación, es un error común creer que a = b es un test booleano. Pero no lo es! Porque el token de Python para testear igualdad es == .
Observar que un test de igualdad es simétrico, pero la asignación no lo es. Por ejemplo, si a == 7 entonces 7 == a. Pero en Python, la sentencia a = 7 es legal pero 7 = a no lo es.
En Python, una asignación puede hacer a dos variables iguales, pero como cada una puede utilizarse en una asignación más adelante, esta igualdad no tiene por qué mantenerse en el tiempo:
a = 5 b = a # Después de ejecutar esta línea, a y b son iguales (valen 5) a = 3 # Después de ejecutar esta línea, a y b ya no son iguales # (a vale 3 pero b sigue valiendo 5)
La tercera línea cambia el valor de a pero no cambia el valor de b, por lo cual ya no son iguales.
En otros lenguajes de programación se usa otro símbolo para la asignación (como <- o :=) para evitar confusiones. Hay quien sostiene que variable no es una buena palabra para describir lo que son y que deberían llamarse asignables. Python sigue la terminología común y el uso de tokens que también utilizan C, C++, Java y C# (es decir, = para asignación y == para chequeo de igualdad - y el llamarlas variables).
7.2) Actualización de variables
Cuando se ejecuta una asignación, la expresión del lado derecho se evalúa primero. Esto produce un valor, que es luego asignado a la variable del lado izquierdo.
Una de las formas más comunes de asignación es una actualización (update), en la que el nuevo valor de la variable depende del antiguo. Por ejemplo, deducir 40 centavos de mi balance actual, o agregar un gol al score de un equipo en un partido de fútbol.
En el siguiente ejemplo, la línea 2 significa: multiplicca por 3 el valor actual de n, súmale 1 y asigna el resultado a la variable n.
n = 5 n = 3 * n + 1
Por lo tanto, tras ejecutar esas dos líneas, el nuevo valor de n será 16.
Si se intenta obtener el valor de una variable que nunca fue asignada, se obtendrá un mensaje de error.
>>> w = x + 1 Traceback (most recent call last): File "<interactive input>", line 1, in <module> NameError: name 'x' is not defined
Antes de poder actualizar una variable, hay que inicializarla en algún paso anterior, por ejemplo con una simple asignación:
>>> goles_anotados = 0 ... >>> goles_anotados = goles_anotados + 1 >>> goles_anotados 1
Líneas del tipo goles_anotados = goles_anotados + 1 son muy comunes. Se llaman incremento de la variable. Si se resta 1, se llama decremento. A veces los programadores hablan de golpear (bumping) la variable, lo que significa lo mismo que incrementarla en 1.
7.3) El loop FOR revisitado
Recordar que el loop for procesa cada item de una lista. En cada turno el item correspondiente es (re)-asignado a la variable del loop, y el cuerpo del loop se ejecuta. Ya vimos este ejemplo en un capítulo anterior (sección 3.3): (L3_for.py)
for f in ["Joe","Zoe","Brad","Angelina","Zuki","Thandi","Paris"]: invite = "Hi " + f + ". Please come to my party on Saturday!" print(invite)
Recorrer todos los items de la lista se llama recorrer (traversing) la lista, o bien un recorrido (traversal).
Escribamos ahora una función que sume todos los elementos en una lista de números. Conviene hacerlo primero a mano para identificar cuáles son los pasos que ejecutamos. Vemos que tenemos que ir guardando una "suma parcial" a medida que vamos sumando, o bien en papel o bien mentalmente o en una calculadora. La necesidad de recordar valores entre un paso y otro es la que justifica la existencia de variables en un programa, así que necesitaremos una variable para ir recordando la "suma parcial". Deberá inicializarse con un valor de cero, y luego necesitamos ir recorriendo los items de la lista e ir sumando sus valores a la "suma parcial". Terminamos con un código así: (L7_suma_de_numeros.py)
def misuma(xs):
""" Suma todos los números en la lista xs, y retorna el total. """
suma_parcial = 0
for x in xs:
suma_parcial = suma_parcial + x
return suma_parcial
# Agregar estos tests al test suite ...
test(misuma([1, 2, 3, 4]) == 10)
test(misuma([1.25, 2.5, 1.75]) == 5.5)
test(misuma([1, -2, 3]) == 2)
test(misuma([ ]) == 0)
test(misuma(range(11)) == 55) # 11 no está incluido en la lista.7.4) La sentencia WHILE
El siguiente fragmento de código muestra cómo se usa la sentencia while: (L7_suma_de_numeros.py)
def sumar_hasta(n):
""" Retorna la suma de 1+2+3 ... n """
ss = 0
v = 1
while v <= n:
ss = ss + v
v = v + 1
return ss
# Tests para sumar_hasta
test(sumar_hasta(4) == 10)
test(sumar_hasta(1000) == 500500)Si uno recuerda que while significa mientras, se puede leer casi literalmente el código (en inglés o en español) y entender lo que hace. Significa: mientras que v sea menor o igual que n, continúe ejecutando el cuerpo del loop. Dentro del cuerpo, incrementamos a v en cada paso y acumulamos la suma parcial. Cuando v se haya pasado de n, retornamos la suma obtenida.
Con más precisión, este es el flujo de ejecución de una sentencia while:
- Evaluar la condición del while, obteniendo un valor que o bien es verdadero o bien es falso.
- Si el valor es False, salir de la sentencia while y ejecutar la primera sentencia siguiente (en nuestoro caso, la línea return)
- Si el valor es True, ejecutar cada una de las sentencias del body y luego volver a ejecutar la sentencia while.
El cuerpo consiste en todas sentencias indentadas luego de la línea while.
Observar que si la condición del loop es falsa la primera vez, las sentencias del cuerpo del loop no serán nunca ejecutadas.
El cuerpo del loop debería cambiar el valor de una o más variables para que eventualmente la condición se vuelva False y el loop termine. De lo contrario el loop se repetirá eternamente, lo que se conoce como loop infinito. Es un viejo chiste entre programadores que las instrucciones de los frascos de shampoo, "hacer espuma, enjuagar, repetir" son un loop infinito.
En nuestro caso, podemos probar que el loop terminará, porque sabemos que el valor n es finito, y podemos ver que el valor de v se incrementa a cada paso del loop, así que tarde o temprano superará a n. En otros casos no es tan obvio, e incluso es imposible en algunos casos, saber si el loop va a terminar o no.
Lo que se ve de inmediato es que el loop while exige más trabajo de parte del programador si se lo compara con un for loop que cumpliera la misma función. En un loop while uno tiene que manejar la variable del loop por sí mismo: darle un valor inicial, testear si se completaron las iteraciones, y también asegurarse de que dicha variable cambie en el cuerpo del loop, para que sea posible su terminación. Para compararlos, esta es una función que hace lo mismo que la anterior, pero mediante un for: (L7_suma_de_numeros.py)
def sumar_hasta_version_for(n):
""" Retorna la suma de 1+2+3 ... n """
ss = 0
for v in range(n+1):
ss = ss + v
return ssObservar el (no tan obvio a primera vista) llamado a range(n+1), que asegura que se tomen todos los valores hasta n (ya que range va hasta un valor igual a uno menos del valor que recibe como argumento). Sería fácil cometer un error al utilizar un loop for en este caso, pero nuestra suite de tests aplicada a la función nos garantiza que seguimos devolviendo los valores correctos.
Entonces, ¿por qué tener dos tipos de loop si for se ve más fácil? El próximo ejemplo muestra un caso en que realmente necesitamos la flexibilidad y el poder extra que nos da la sentencia while.
7.5) La secuencia 3n + 1 de Collatz
Miremos a una simple secuencia que ha fascinado y despistado a los matemáticos por años. Aun no han logrado contestar algunas preguntas sencillas sobre la misma.
La "regla computacional" para crear la secuencia es comenzar con un número n, y generar el siguiente término de la secuencia, o bien dividiendo n a la mitad (si n es par), o bien multiplicándolo por 3 y sumando 1. La secuencia termina cuando n vale 1.
La siguiente función Python implementa el algoritmo: (L7_suma_de_numeros.py)
def seq3np1(n):
""" Imprimir la secuencia 3n+1 a partir de n,
terminando cuando se alcanza el 1.
"""
while n != 1:
print(n, end=", ")
if n % 2 == 0: # n es par
n = n // 2
else: # n es impar
n = n * 3 + 1
print(n, end=".\n")Observar primero que la primera línea print tiene un parámetro extra end=", ". Éste le dice a la función print que continúe el string impreso con lo que sea que elija el programador (en este caso, una coma seguida de un espacio) en vez de un fin de línea. Así, cada vez que algo se imprime en el loop, se continúa imprimiendo en la misma línea y se va separando a los números sucesivos con comas. El llamado al segundo print, por lo tanto, va a imprimir el último número de la lista seguido de un punto y un fin de línea. Hablaremos con más detalle del carácter \n (fin de línea) en el próximo capítulo.
La condición para continuar con el loop es n != 1, por lo cual el loop seguirá corriendo hasta que alcance la condición de terminación (n == 1)
En cada iteración el programa imprime el número n y luego chequea si es par o impar. Si es par, el valor de n se divide por 2 (división entera). Si es impar, el valor se sustituye por n*3 + 1.
Algunos ejemplos de corridas:
>>> seq3np1(3) 3, 10, 5, 16, 8, 4, 2, 1. >>> seq3np1(19) 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. >>> seq3np1(21) 21, 64, 32, 16, 8, 4, 2, 1. >>> seq3np1(16) 16, 8, 4, 2, 1.
Ya que en ocasiones n aumenta y en ocasiones disminuye, no hay una prueba obvia de que alcanzará el valor 1 (de forma que el programa termine). Para algunos valores particulares de n podemos probar que terminará. Por ejemplo, si el valor inicial es una potencia de 2, entonces el valor de n será par en todos los pasos de la iteración hasta alcanzar el valor 1. Los ejemplos anteriores terminan todos con la secuencia 16, 8, 4, 2, 1. Prueba a buscar un número pequeño que necesite más de 100 pasos para terminarse.
- Respuesta: el número 73 produce el siguiente output: 73, 220, 110, 55, 166, 83, 250, 125, 376, 188, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1. (habrá otro menor que 73 que lo cumpla?)
Dejando de lado los casos particulares, la pregunta interesante fue planteada en primer lugar por el matemático alemán Lothar Collatz: la conjetura de Collatz (también conocida como conjetura 3n + 1) sostiene que la secuencia termina para todos los enteros positivos n. Hasta ahora nadie ha podido probar que la conjetura sea verdadera o falsa (una conjetura es una afirmación que parece ser cierta y puede ser cierta, pero nadie ha logrado demostrar aún que lo sea).
Una prueba matemática no es lo mismo que un test o que varios tests. Con computadoras hemos testeados billones de números positivos y todos convergen a 1. Pero eso no es lo mismo que haber probado que con todos funcionará, y un día podría encontrarse un número mucho más grande que los testeados que nunca converja.
Cabe observar que si uno no se detiene en 1, la secuencia queda eternamente encerrada en el ciclo 1, 4, 2, 1, 4, 2, 1, 4, 2, ... Así que una posibilidad (que haría falsa a la conjetura) es que existan otros ciclos que aun no hemos encontrado.
Wikipedia tiene un artículo muy completo sobre la conjetura de Collatz. La secuencia recibe también otros nombres (secuencia de granizo, números maravillosos, etc.). En ese artículo se mantienen al día en cuanto a cuál es el mayor número hasta el que se ha testeado exitosamente.
Cómo elegir entre for y while.
- Usa un loop for si sabes, de antemano, cuál es el máximo número de veces que deberás iterar. Por ejemplo, al recorrer una lista de elementos, se sabe que el máximo número de iteraciones será la cantidad de elementos de la lista. O si se necesita imprimir la tabla de multiplicar del 12, sabemos de antemano cuántos números habremos de imprimir. Así que todo problema del tipo "iterar este modelo del tiempo por 1000 ciclos", "buscar en esta lista de palabras" o "encontrar todos los números primos menores que 10000" sugieren que el loop for es la mejor opción.
- En cambio, si es necesario repetir una computación hasta que cierta condición se cumpla, y no se puede saber de antemano cuándo (o incluso si) esto ocurrirá, como en el ejemplo del problema 3n + 1, entonces es más conveniente un loop while.
Llamamos iteración definida a las del primer tipo (en que conocemos de antemano un límite para la cantidad de iteraciones requeridas). Y a las del segundo tipo iteraciones indefinidas (no sabemos cuántas serán necesarias de antemano e incluso en algunos casos no podemos asegurar que vaya a terminar).
7.6) Trazabilidad de un programa
Para escribir programas efectivos y construir un buen modelo conceptual de ejecución de programas, el programador necesita desarrollar su habilidad para rastrear la ejecución del mismo. Rastrear (trace) implica pensar como la computadora y seguir el flujo de ejecución a través de una corrida del programa, llevando la cuenta del valor de las variables a medida que el programa se ejecuta.
Como ejemplo, hagamos el rastreo del llamado seq3np1(3) de la sección previa. Comenzamos con la variable n (el parámetro), con el valor inicial 3. Como 3 no es igual a 1, ejecutamos el body del while. Se imprime el 3 y se evalúa 3 % 2 == 0. Como evalúa a False, vamos a la rama else y evaluamos 3 * 3 + 1 para asignar el resultado a n.
Para llevar la cuenta a medida que uno rastrea a mano el programa, conviene hacer una tabla de columnas en una hoja de papel (cada columna corresponde a una variable, más otra columna para el output). Nuestro rastreo en este caso comienza viéndose así:
n output printed so far -- --------------------- 3 3, 10 Como 10 != 1, evalúa a True, el body del while vuelve a ejecutarse, se imprime 10, y como 10 % 2 == 0 es True, se ejecuta la rama if y n se convierte en 5. Al final del rastreo del programa completo tenemos algo así: n output printed so far -- --------------------- 3 3, 10 3, 10, 5 3, 10, 5, 16 3, 10, 5, 16, 8 3, 10, 5, 16, 8, 4 3, 10, 5, 16, 8, 4, 2 3, 10, 5, 16, 8, 4, 2, 1 3, 10, 5, 16, 8, 4, 2, 1.
El rastreo puede ser un poco tedioso y sujeto a errores (es la razón por la que hacemos que las propias computadoras lo hagan!), pero es una habilidad esencial que debe tener el programador. De esta traza podemos aprender muchísimo sobre el modo en que funciona nuestro programa. Podemos ver que apenas se convierte en una potencia de 2, por ejemplo, el programa requerirá log2(n) ejecuciones del cuerpo del loop para terminar. Podemos ver también que el 1 final nunca será impreso como output dentro del body del loop (sino con el print especial que dibuja un punto en vez de una coma).
Rastrear un programa tiene que ver, por supuesto, con aquello de ejecutar paso a paso el código e ir inspeccionando las variables. Permitir que la computadora haga el paso a paso en vez de hacerlo nosotros mismos está menos sujeto a error y es más rápido. Además, cuando se complique el programa, es posible que haya que ejecutar millones de pasos antes de alcanzar la parte del código que realmente nos interesa, así que el rastreo manual se vuelve imposible. Ser capaz de establecer un breakpoint donde se hace necesario uno es mucho más efectivo. Por lo cual te recomendamos encarecidamente aprender bien a utilizar tu entorno de programación (PyScripter, en este curso) para sacarle el mayor provecho posible a las herramientas que ofrece.
También hay numerosas herramientas de visualización que permiten rastrear y comprender pequeños fragmentos de código Python.
Ya advertimos contra las funciones charlatanas, pero hemos usado una aquí. A medida que aprendamos más sobre Python, veremos cómo podemos generar una lista de valores para ir guardando la secuencia, en vez de tener que hacer que la función la vaya imprimiendo. Hacer esto eliminará la necesidad de utilizar esos incómodos print intercalados en la lógica del programa, y hará a la función más útil hacia afuera.
7.7) Contando dígitos
La siguiente función cuenta la cantidad de dígitos decimales en un número entero: (L7_suma_de_numeros.py)
def cantidad_digitos(n):
cantidad = 0
while n != 0:
cantidad = cantidad + 1
n = n // 10
return cantidadUn llamado a print(cantidad_digitos(710)) imprimirá un 3.
Esta función es un ejemplo de uso de un importante patrón de computación llamado contador. La variable cantidad inicializada en 0 y luego incrementada cada vez que el loop es ejecutado es un típico contador, que guarda la cantidad de veces que el cuerpo del loop fue ejecutado (lo cual equivale a la cantidad de dígitos del número pasado como parámetro).
Si sólo queríamos contar dígitos que fueran 0 o 5, hubiéramos agregado un condicional antes del incremento, así: (L7_suma_de_numeros.py)
def cantidad_digitos_cero_y_cinco(n):
cantidad = 0
while n > 0:
digito = n % 10
if digito == 0 or digito == 5:
cantidad = cantidad + 1
n = n // 10
return cantidadConfirmar que test(cantidad_digitos_cero_y_cinco(1055030250) == 7) pasa el test:
Observar, sin embargo, que test(num_digits(0) == 1) falla. Explicar por qué.
- Respuesta: es porque el while supone que n > 0, lo que no se da si n == 0. O sea, que el script presupone que el número no inicia con un 0, lo cual sería correcto para cualquier número entero bien formateado excepto el número 0.
Consideras que esto es un bug del código, o de la especificación, o de las expectativas, o de los tests?
- Respuesta: es claramente un bug del código. Podría considerarse de la especificación o de las expectativas, pero sería discutible. Es indiscutible en cambio que hay un problema en el código, al no tratar especialmente el caso n = 0.
7.8) Asignaciones abreviadas
Es tan común incrementar variables que Python ofrece una sintaxis especial para hacerlo:
>>> count = 0 >>> count += 1 >>> count 1 >>> count += 1 >>> count 2
La expresión count += 1 es una abreviación de count = count + 1. Llamamos al operador "plus-equals" ("más-igual"). Se puede incrementar de a otros saltos, no sólo 1:
>>> n = 2 >>> n += 5 >>> n 7
Existen abreviaciones similares para los demás operadores aritméticos: -=, *=, /=, //= y %=
>>> n = 2 >>> n *= 5 >>> n 10 >>> n -= 4 >>> n 6 >>> n //= 2 >>> n 3 >>> n %= 2 >>> n 1
7.9) Ayuda y meta-notación
Python incluye una extensa documentación para sus funciones built-in y sus librerías. El modo de acceder a esa ayuda depende del entorno de programación. En PyScripter hay que hacer click en Help y seleccionar Manuales de Python. Como ejemplo, podemos buscar lo que dice la ayuda a propósito de la función range. Encontramos algo así:
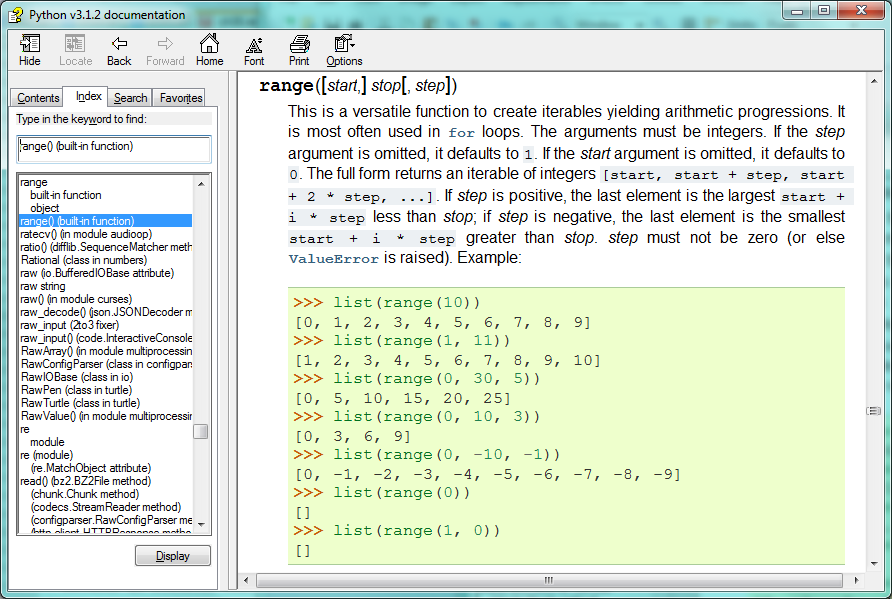
Observación: en el PyScripter actual range figura como una built-in-class y en vez de tener un único cabezal con start y step entre corchetes, tiene dos cabezales: uno en que sólo está stop, y otro en que start y stop son obligatorios y step va entre corchetes.
Los paréntesis rectos (corchetes) en la definición de la función range son ejemplos de meta-notación (notación que sirve para describir y documentar la notación Python, pero que no es parte de ella). En esta documentación, los paréntesis rectos significan que el argumento es opcional (el programador que llama a la función puede omitirlos). Por lo tanto lo que nos dice esa definición de range es que stop es un parámetro obligatorio (siempre tiene que estar), pero puede tener un start opcional (seguido de una coma, en caso de estar presente) y puede también tener un step opcional (precedido por una coma, en caso de estar presente).
Los ejemplos de la ayuda muestran que range puede tener 1, 2 o 3 argumentos. La lista puede comenzar por cualquier valor y dar saltos de cualquier valor. Por defecto se empieza en cero y se salta de a 1. En viejas versiones de Python los argumentos debían ser enteros (de tipo int), pero en la versión actual se acepta cualquier objeto que implemente el método especial __index__.
Otra meta-notación que se encuentra con frecuencia es el uso de negrita y cursiva. La negrita significa que hablamos de tokens (palabras clave o símbolos), las cuales deben ir en el código Python exactamente como son, mientras que la cursiva indica "poner aquí algo de este tipo". Por lo tanto, en la descripción:
for variable in lista:
Se nos está indicando que for e in deben ir exactamente como están, y que podemos sustituir variable y lista por cualquier variable o lista válidas que tengamos en nuestro programa.
La siguiente descripción (simplificada) de la función print muestra otro ejemplo de meta-notación en que los tres puntos (...) significan que se pueden tener tantos objetos como se quieran (incluso se puede tener ninguno) separados por comas:
print( [objeto, ...] )
La meta-notación nos da una forma concisa y poderosa de describir el patrón de una cierta sintaxis o funcionalidad.
7.10) Tablas
Los loops son muy útiles, entre otras cosas, para generar tablas. Antes de que las computadoras fueran accesibles, la gente debía calcular logaritmos, senos y cosenos (y otras funciones matemáticas) a mano. Para facilitar el trabajo, se vendían libros con grandes tablas que contenían los valores de dichas funciones. La creación de estas tablas era una actividad lenta y tediosa, y el resultado tendía a estar plagado de errores.
Cuando aparecieron las computadoras, una de las primeras reacciones fue "qué bueno! podemos usar las computadoras para generar tablas, y ya no tendremos errores!". Esto resultó ser cierto, pero no muy visionario. En cuestión de años las computadoras y calculadoras fueron tan populares que los libros que traían tablas se volvieron completamente obsoletos.
Sin embargo, para ciertas operaciones las computadoras usan tablas de valores para obtener un valor aproximado y luego hacen computaciones para mejorar dicha aproximación. En algunos casos han habido errores en las tablas subyacentes, siendo un caso famoso el error que venía en el procesador Pentium para la operación de división de números float.
Si bien una tabla de logaritmos ya no es tan útil como lo era en el pasado, nos va a servir como ejemplo para implementar iteraciones. El siguiente programa produce dos columnas: a la izquierda los números del 0 al 12 y a la derecha las correspondientes potencias de 2 para dichos valores. (L7_suma_de_numeros.py - función tabla_potencias_2)
for x in range(13): # Generate numbers 0 to 12 print(x, "\t", 2**x)
El string "\t" representa un carácter de tabulación. La barra invertida en "\t" señala el principio de una secuencia de escape. Las secuencias de escape se usan para representar caracteres invisibles como tabulación y fin de línea. La secuencia \n representa un fin de línea.
Una secuencia de escape puede aparecer en cualquier punto de un string. En nuestro ejemplo el tabulador aparece solo, pero no es necesario que sea así. ¿Cómo piensas que se representaría una barra invertida en un string? (respuesta: con un \\, doble barra invertida)
A medida que los caracteres y strings se muestran en pantalla, un marcador invisible llamado cursor lleva la cuenta de la posición en que irá el nuevo carácter. Después de una línea print, el cursor va generalmente al inicio de la línea siguiente.
El carácter tabulación mueve el cursor hacia la derecha hasta que alcanza el siguiente tab stop. Las tabulaciones son útiles para alinear columnas de texto, como se ve en el output del programa anterior:
0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 11 2048 12 4096
A causa de los tabs entre columnas, la posición de la segunda columna no se altera a medida que cambia la cantidad de caracteres en la primera. Obviamente lo anterior tiene un límite práctico, que es no pasar de cierto límite con el ancho de la primera columna.
7.11) Tablas bidimensionales
Una tabla bidimensional es una tabla en que se lee el valor en la intersección de una fila y una columna. La tabla de multiplicar es el ejemplo más conocido. Supongamos que queremos imprimir las tablas de multiplicar para los valores del 1 al 10. Empecemos por imprimir todos los múltiplos de 2, así: (L7_suma_de_numeros.py - función tabla_multiplicar_2)
for i in range(1, 11): print(2 * i, end=" ") print()
Aquí usamos la función range pero haciendo comenzar la secuencia en 1. A medida que se ejecuta el loop, el valor de i va cambiando de 1 a 10. Cuando se recorrieron todos los valores, el loop termina. A cada paso del loop va imprimiendo 2 * i seguido por 3 espacios.
Como ya habíamos visto, el end=" " de la función print elimina el carácter fin de línea y usa 3 espacios en su lugar. Cuando se completa el loop, el llamado final a print() imprime una nueva línea con lo cual se pasa a la línea siguiente.
El output del programa es así:
2 4 6 8 10 12 14 16 18 20
Hasta ahora todo bien. El siguiente paso es encapsular y generalizar.
7.12) Encapsulación y generalización
La encapsulación consiste en poner una pieza de código dentro de una función, con lo cual podemos aprovechar todas las ventajas que ofrece una función. Ya vimos algunas ventajas de la encapsulación, por ejemplo en el ejemplo es_divisible del capítulo anterior.
La generalización implica tomar algo específico, como imprimir los múltiplos de 2, y convertirlo en algo más general, como imprimir los múltiplos de cualquier entero.
La siguiente función encapsula al loop visto en la sección anterior, y lo generaliza para imprimir múltiplos de n (siendo n cualquier entero). (L7_suma_de_numeros.py - función tabla_multiplicar)
def tabla_multiplicar(n): for i in range(1, 11): print(n*i, end=" ") print()
Para encapsular, lo único que tuvimos que hacer fue agregar la primera línea que declara el nombre de la función. Para generalizar, sólo tuvimos que reemplazar el número 2 por el parámetro n.
Si llamamos esta función con el parámetro 2 obtenemos el mismo resultado que antes. Con el parámetro 3 obtendríamos la tabla del 3, o con el 7 la tabla del 7, así:
7 14 21 28 35 42 49 56 63 70
Podríamos entonces imprimir todas las tablas de multiplicar llamando a esta función para todos los n del 1 al 10 (L7_suma_de_numeros.py - función tablas_multiplicar)
for i in range(1, 11): tabla_multiplicar(i)
Observar cómo es similar este loop al que ya teníamos en la función tabla_multiplicar. Lo único que hicimos fue reemplazar la línea print con un llamado a función.
El output de este programa es una tabla de multiplicar:
1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 12 14 16 18 20 3 6 9 12 15 18 21 24 27 30 4 8 12 16 20 24 28 32 36 40 5 10 15 20 25 30 35 40 45 50 6 12 18 24 30 36 42 48 54 60 7 14 21 28 35 42 49 56 63 70 8 16 24 32 40 48 56 64 72 80 9 18 27 36 45 54 63 72 81 90 10 20 30 40 50 60 70 80 90 100
7.13) Más encapsulación
Para ilustrar la encapsulación una vez más, tomemos el código de la sección anterior y pongámoslo en una función: (L7_suma_de_numeros.py - función tablas_multiplicar)
def tablas_multiplicar(): for i in range(1, 11): tabla_multiplicar(i)
Este proceso es un plan de desarrollo habitual. Comenzamos escribiendo líneas de código fuera de una función, directamente en el intérprete. Cuando logramos que el código funcione, lo extraemos y encapsulamos en una función.
Este procedimiento es muy útil si uno no sabe de antemano cómo dividir el programa en funciones. Este método permite ir diseñando el programa a medida que se lo va desarrollando.
7.14) Variables locales
Podrías preguntarte cómo es que podemos usar la misma variable i en las dos funciones tabla_multiplicar y tablas_multiplicar. ¿No causa problemas cuando una de las funciones cambia su valor?
La respuesta es que no, porque la i de tabla_multiplicar y la i de tablas_multiplicar no son la misma variable.
Las variables que se crean dentro de una función son locales, es decir, no se puede acceder a ellas fuera de la función. Por lo tanto podemos utilizar múltiples variables con el mismo nombre, siempre y cuando no estén en la misma función.
Python examina todas las sentencias en una función. Si una de ellas asigna un valor a una variable, Python hace que dicha variable sea local.
El diagrama de pila (stack diagram) para este programa muestra que las dos variables llamadas i no son la misma variable. Pueden referirse a distintos valores, y el hecho de que una cambie no afecta a la otra.
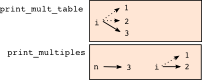
- (en esta figura, "print_mult_table" corresponde a tablas_multiplicar, y "print_multiples" a tabla_multiplicar)
El valor de i en tablas_multiplicar va cambiando de 1 a 10. En el diagrama mostrado arriba estamos en el momento en que vale 3. En el siguiente paso del loop va a valer 4. A cada paso del loop, tablas_multiplicar llama a tabla_multiplicar, con el valor actual de i como argumento. Dicho valor es asignado en tabla_multiplicar al parámetro n.
Dentro de tabla_multiplicar, el valor de i va de 1 a 10. En el diagrama estamos en el momento en que vale 2. Cambiar esta variable no tiene efecto sobre el valor de la i de tablas_multiplicar.
Es común y perfectamente legal tener distintas variables locales con el mismo nombre. En particular, nombres como i y j se usan con frecuencia como variables de loops. Si evitas usar esos nombres en una función porque ya los usaste en otro, a la larga te quedarás sin nombres y el programa será muy difícil de leer.
7.15) La sentencia BREAK
La sentencia break se usa para abandonar de inmediato el cuerpo de un loop. La sentencia que se ejecuta después de un break es la inmediatamente posterior al cuerpo del loop.
Por ejemplo: (L7_suma_de_numeros.py - ejemplo_break)
for i in [12, 16, 17, 24, 29]:
if i % 2 == 1: # Si el número es impar
break # ... salir de inmediato del loop
print(i)
print("ya hemos salido del loop")Esto imprime:
12 16 ya hemos salido del loop
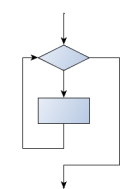
Los loops pre-test - comportamiento estándar de este tipo de loops
- Los loops for y while hacen el test al principio, antes de ejecutar el body. Por eso se llaman loops pre-test.
- Las herramientas break y return nos permiten adaptar ese comportamiento en casos específicos.
7.16) Otros tipos de loops
En ocasiones querremos tener un loop mid-test (el cual hace el test de salida en la mitad del loop). O un loop post-test (el cual hace su test de salida al final del loop). Otros lenguajes tienen diferentes sintaxis y palabras clave para estos casos, pero Python sólo usa una combinación de while e if condición: break para conseguir el efecto deseado.
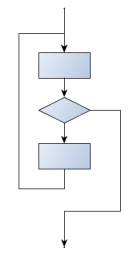
Un ejemplo típico es un problema en que el usuario tiene que introducir números que han de sumarse. Para indicar que no hay más inputs, el usuario ingresa un valor especial, por ejemplo el valor -1 o el string vacío. Esto necesita de un loop mid-test que permita ingresar el siguiente número, luego chequee si hay que salir o bien procese el siguiente número. (L7_suma_de_numeros.py - mid_test_loop)
total = 0
while True:
respuesta = input("Ingrese el número siguiente. (Deje en blanco para terminar)")
if respuesta == "":
break
total += int(respuesta)
print("La suma total de los números ingresados es ", total)Trata de comprender por qué esto corresponde a un loop mid-test. Antes del if respuesta == "" hay código útil y después también, todo como parte del body. Y si la respuesta es "" entonces se sale del loop de inmediato, antes de que comience la siguiente iteración.
El while expresión booleana: utiliza la expresión booleana para decidir si iterar otra vez. Con el while True: estamos diciendo itera el body indefinidamente. Este es un uso convencional que la mayor parte de los programadores reconocerán de un golpe de vista. Ya que esa condición nunca terminará el loop (es un test dummy) el programador se las debe arreglar para salirse del loop (con un break) de otra forma. Un compilador bien diseñado comprenderá que la línea while True: es un falso test (fake test) así que ni siquiera generará un test, y no pondrá un rombo inicial en el diagrama de flujo correspondiente al while.
De modo similar, con sólo mover el if condicion: break al final del cuerpo del loop habremos creado un patrón para un loop post-test. Éstos se usan cuando quieres estar seguro de que el cuerpo del loop se ejecute al menos una vez (dado que el primer test sólo ocurre al final del body). Es útil, por ejemplo, cuando se juega un juego interactivo contra el usuario - siempre queremos al menos jugar un juego:
while True:
jugar_el_juego_una_vez()
respuesta = input("Jugar otra vez? (sí o no)")
if respuesta != "sí":
break
print("Hasta la vista!")Consejo: En todo loop, piensa dónde quieres que ocurra el test de exit
- Una vez que decidiste que vas a necesitar un loop para que algo ocurra, es importante pensar sobre la condición de terminación: ¿cuándo quiero que se termine de iterar?
- luego decidir si se quiere testear antes de la primera iteración (y de las demás), o al final de la primera (y de las demás), o en el medio.
- Los programas interactivos que requieren input del usuario o datos leídos de archivos suelen tener que salir en el medio o al final de una iteración (cuando queda claro que ya no quedan datos a procesar o que el usuario ya no quiere jugar)
7.17) Un ejemplo
El siguiente programa implementa un juego de adivinar (deducir) el número: (L7_suma_de_numeros.py - adivinar_el_numero)
import random # Veremos los números random (aleatorios) con detalle más adelante
...
def adivina_el_numero():
rng = random.Random()
numero = rng.randrange(1, 1000) # Obtener un número random en el intervalo [1 ; 1000).
intentos = 0
msg = ""
while True:
intento = int(input(msg + "\nAdivina mi número entre 1 y 1000: "))
intentos += 1
if intento > numero:
msg += str(intento) + " es demasiado grande.\n"
elif intento < numero:
msg += str(intento) + " es demasiado pequeño.\n"
else:
break
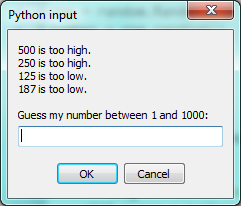
input("\n\nMuy bien! Lo adivinaste en {0} intentos!\n\n".format(intentos))Este programa utiliza la ley matemática de tricotomía (dados dos números a y b, entonces se cumple una de estas tres: a < b, a > b o a == b).
En la línea final se utiliza un input por más que no hagamos nada con el valor que ingresa el usuario. Esto es legal en Python, y tiene el efecto de mostrar un diálogo que evita que el programa termine hasta que el usuario haga click en el botón "Ok". Los programadores usan con frecuencia el truco de agregar un input final a los scripts, con el fin de mantener la ventana abierta.
También vemos la utilización de la variable msg, que inicialmente es un string vacío y se va extendiendo con más líneas a medida que el programa se ejecuta: esto permite que el programa muestre su feedback completo en el mismo lugar en que pedimos al usuario que haga un nuevo intento.
7.18) La sentencia CONTINUE
La sentencia continue es una sentencia de control de flujo que hace que el programa salte de inmediato el procesamiento del resto del body del loop, pero sólo para la iteración actual. El loop continúa y se ejecutan las demás iteraciones. (L7_suma_de_numeros.py - ejemplo_continue)
def ejemplo_continue():
for i in [12, 16, 17, 24, 29, 30]:
if i % 2 == 1: # Si el número es impar
continue # ... no procesarlo
print(i)
print("terminamos")Esto imprime:
12 16 24 30 done
7.19) Más generalizaciones
Como un nuevo ejemplo de generalización, imaginemos que queremos imprimir tablas de multiplicar de 1 hasta N, donde N es cualquier natural - y no sólo de 1 hasta 10 como en la vieja versión de tablas_multiplicar(). Para conseguirlo, agregamos un parámetro a la función, que indique la cantidad de filas y columnas: (L7_suma_de_numeros.py - tablas_multiplicar(high))
def tablas_multiplicar(high): for i in range(1, high+1): tabla_multiplicar(i)
Hemos reemplazado el valor 11 con el nuevo high+1. Si llamamos a la función con argumento 12, imprime:
1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 12 14 16 18 20 3 6 9 12 15 18 21 24 27 30 4 8 12 16 20 24 28 32 36 40 5 10 15 20 25 30 35 40 45 50 6 12 18 24 30 36 42 48 54 60 7 14 21 28 35 42 49 56 63 70 8 16 24 32 40 48 56 64 72 80 9 18 27 36 45 54 63 72 81 90 10 20 30 40 50 60 70 80 90 100 11 22 33 44 55 66 77 88 99 110 12 24 36 48 60 72 84 96 108 120
Eso está bien, salvo por el hecho de que probablemente hubiéramos preferido que la tabla fuera cuadrada (con la misma cantidad de filas y columnas). Para conseguirlo, debemos también agregar un parámetro a tabla_multiplicar(n) que indique el tamaño de la tabla en cuestión. Nos queda así: (L7_suma_de_numeros.py - función tabla_multiplicar(n, high))
def tabla_multiplicar(n, high):
for i in range(1, high+1):
print(n*i, end=" ")
print()
def tablas_multiplicar(high):
for i in range(1, high+1):
tabla_multiplicar(i, high)Observar que hemos agregado un nuevo parámetro a tabla_multiplicar, y una vez reflejado el cambio en la definición de dicha función, tuvimos que llamarla con dos argumentos desde la otra función, tablas_multiplicar.
Ahora obtenemos la siguiente tabla cuadrada de 12*12:
1 2 3 4 5 6 7 8 9 10 11 12 2 4 6 8 10 12 14 16 18 20 22 24 3 6 9 12 15 18 21 24 27 30 33 36 4 8 12 16 20 24 28 32 36 40 44 48 5 10 15 20 25 30 35 40 45 50 55 60 6 12 18 24 30 36 42 48 54 60 66 72 7 14 21 28 35 42 49 56 63 70 77 84 8 16 24 32 40 48 56 64 72 80 88 96 9 18 27 36 45 54 63 72 81 90 99 108 10 20 30 40 50 60 70 80 90 100 110 120 11 22 33 44 55 66 77 88 99 110 121 132 12 24 36 48 60 72 84 96 108 120 132 144
Cuando se generaliza una función de forma apropiada, se puede obtener un programa con capacidades que inicialmente no estuvieron planeadas. Por ejemplo, se puede observar que, por el hecho de que ab = ba, todas las entradas en la tabla aparecen dos veces. Se puede ahorrar tinta imprimiendo sólo la mitad de la tabla. Para conseguirlo, basta con cambiar el llamado tabla_multiplicar(i, high) por un llamado tabla_multiplicar(i, i) en la última línea de tablas_multiplicar, y se obtiene esta salida: (L7_suma_de_numeros.py - función tablas_multiplicar(high))
1 2 4 3 6 9 4 8 12 16 5 10 15 20 25 6 12 18 24 30 36 7 14 21 28 35 42 49 8 16 24 32 40 48 56 64 9 18 27 36 45 54 63 72 81 10 20 30 40 50 60 70 80 90 100 11 22 33 44 55 66 77 88 99 110 121 12 24 36 48 60 72 84 96 108 120 132 144
7.20) Funciones
A estas alturas ya hemos mencionado todas las razones por las cuales las funciones son útiles. Recordemos algunas:
- Capturan tu subdivisión mental del problema. Dividir tareas complejas en subtareas y darle a esas subtareas un nombre comprensible es una técnica poderosa. Recordemos el ejemplo con el que ilustramos el loop post-test: supusimos que teníamos una función llamada jugar_el_juego_una_vez. Esa subdivisión nos permitió dejar de lado los detalles del juego en particular (da lo mismo si es un juego de cartas, el tateti o un juego de rol) y enfocarnos en una parte aislada de la lógica de nuestro programa: el momento en que se permite al jugador decidir si va a jugar de nuevo o no.
- Dividir un programa grande en funciones permite separar partes del programa, testearlas independientemente y cuando ya funcionan, combinarlas en un todo.
- Las funciones facilitan el uso de la iteración.
- Las funciones bien diseñadas suelen ser útiles en varios programas. Una vez que se escribió y testeó una, queda disponible para su reutilización.
- Relacionado con los puntos anteriores: encapsular código en una función es mejor que cortar y pegar trozos porque tenemos, por ejemplo, variables locales (que evitan conflictos de nombres)
7.21) Datos apareados
Ya vimos listas de nombres y de números en Python. Vamos a ver ahora un modo más avanzado de representar datos. Crear un par en Python es tan fácil como poner el par entre paréntesis:
año_nacimiento = ("José Gervasio Artigas", 1764)Podemos poner varios pares en una lista de pares:
celebs = [("Brad Pitt", 1963), ("Jack Nicholson", 1937), ("Justin Bieber", 1994)]Aquí hay un pequeño ejemplo de lo que podemos hacer con datos estructurados de esta forma. Comencemos por imprimirlos:
print(celebs) print(len(celebs))
Obtenemos esto:
[("Brad Pitt", 1963), ("Jack Nicholson", 1937), ("Justin Bieber", 1994)]
3Observar que la lista sólo tiene 3 elementos, siendo cada elemento un par.
Ahora queremos imprimir los nombres de las celebridades nacidas antes de 1980 (L7_suma_de_numeros.py - función print_celebs)
for (nm, yr) in celebs: if yr < 1980: print(nm)
Obtenemos este output:
Brad Pitt Jack Nicholson
Este código ilustra algo que aun no habíamos visto en el loop for. En vez de usar una variable de control, usamos un par de nombres de variable. El cuerpo del loop se ejecuta 3 veces, una por cada par en la lista, y en cada iteración a ambas variables se les asignan valores del par de datos que se está manejando.
7.22) Loops anidados para datos anidados
Ahora veamos una lista de datos aun más compleja estructuralmente. Tenemos una lista de estudiantes. Cada estudiante se representa como un par que contiene, en su primer elemento, el nombre del estudiante, y en el segundo, la lista de materias que se inscribió para cursar. Algo así: (L7_suma_de_numeros.py - función print_estudiantes)
estudiantes = [
("Juan", ["Informática", "Física"]),
("Dani", ["Matemáticas", "Informática", "Estadística"]),
("Jess", ["Informática", "Contabilidad", "Economía", "Administración"]),
("Sarah", ["Informática", "Contabilidad", "Economía", "Filosofía"]),
("Zaira", ["Sociología", "Economía", "Derecho", "Estadísticas", "Música"])]Aquí hemos asignado una lista de 5 elementos a la variable estudiantes. Ahora imprimimos cada nombre de estudiante y la cantidad de cursos a los que se inscribió cada uno de ellos:
#Imprimir la lista de estudiantes con la cantidad de materias a las que se inscribieron for (nombre, cursos) in estudiantes: print(nombre, "se inscribió en", len(cursos), "cursos")
Python devuelve el siguiente output:
Juan se inscribió en 2 cursos Dani se inscribió en 3 cursos Jess se inscribió en 4 cursos Sarah se inscribió en 4 cursos Zaira se inscribió en 5 cursos
Ahora querríamos saber cuántos estudiantes están cursando Informática. Llevaremos la cuenta en un contador, y para cada estudiante debemos recorrer la segunda lista para ver si "Informática" está allí. Obtenemos un código como este: (L7_suma_de_numeros.py - función print_estudiantes)
# Contar cuántos estudiantes estudian Informática
counter = 0
for (nombre, cursos) in estudiantes:
for c in cursos: # Un loop anidado!
if c == "Informática":
counter += 1
print("El número de estudiantes que cursan Informática es", counter)Vemos en el código de esta función un ejemplo de loop anidado: el loop que recorre la lista de cursos de cada estudiante está anidado dentro del loop que recorre a todos los pares que representan a los estudiantes. Python devuelve:
El número de estudiantes que cursan Informática es 4
Prueba a hacer una lista con tus propios datos de interés (por ejemplo tus discos favoritos con una lista de canciones para cada uno, o escritores favoritos con una lista de obras, o equipos de fútbol favorito con una lista de torneos ganados). Y luego hacer preguntas del tipo: ¿Qué campeonatos fueron ganados por el Manchester City? ¿Qué canciones vienen en el disco The Wall the Pink Floyd? (es una tarea para el estudiante)
7.23) El método de Newton para hallar raíces cuadradas
Los loops se usan con frecuencia en programas que computan resultados numéricos partiendo de un resultado aproximado y mejorándolo en cada iteración.
Por ejemplo, antes de tener calculadoras o computadoras, la gente necesitaba calcular las raíces cuadradas a mano. Newton usó un método particular (hay evidencia que sugiere que dicho método ya era conocido antes de que él lo utilizara, pero por siglos se le ha atribuido y por eso lleva su nombre). Supongamos que quieres conocer la raíz cuadrada de n. Si comienzas con cualquier aproximación, puedes obtener una aproximación más precisa (más cercana a la respuesta correcta) utilizando esta fórmula:
mejor_aproximacion = (aproximacion + n/aproximacion)/2
Si pruebas a repetir esta cuenta varias veces (por ejemplo, usando una calculadora) verás que en cada iteración obtienes una respuesta más cercana a la raíz cuadrada correcta. ¿Puedes comprender por qué en cada paso te aproximas a la respuesta correcta? Una de las mejores características de este famoso algoritmo es que converge muy rápido hacia la respuesta correcta: una gran ventaja si hay que calcularlo a mano! (sería interesante averiguar o calcular qué tan rápido converge)
Usando esta fórmula dentro de un loop e iterando una cantidad suficiente de veces, podemos obtener una buena aproximación a la raíz cuadrada de cualquier número. Este es un ejemplo de iteración indefinida: no sabemos de antemano cuántas veces tendremos que repetir la iteración, sólo lo haremos hasta que obtengamos cierto nivel de precisión. En este ejemplo, nos detendremos cuando la diferencia entre la aproximación vieja y la nueva difieran en menos de cierta cantidad límite mínima que hayamos fijado de antemano.
Lo ideal sería que la nueva y la vieja aproximación coincidan en algún paso de la iteración (eso querría decir que llegamos a la solución exacta). Pero la "igualdad exacta" es una noción que introduce múltiples dificultades en aritmética computacional cuando trabajamos con números reales. Como los números reales no son representados con exactitud, para determinar si dos números a y b son "iguales" o "suficientemente cercanos" necesitamos formular el test de parada con una pregunta del tipo "está a lo suficientemente cerca de b"? Esta condición de parada puede codificarse así:
if abs(a-b) < 0.001: # Se pueden tomar números menores que 0.001 para incrementar la precisión break
Observar que tomamos el valor absoluto de la diferencia entre a y b!
El algoritmo de Newton es también un ejemplo en que es conveniente un loop mid-test. El código de la función queda así: (L7_suma_de_numeros.py - función raiz_newton)
def raiz_newton(n): aproximacion = n/2.0 # Comenzamos con una suposición "a lo bruto" - puede ser esta o cualquier otra while True: mejor = (aproximacion + n/aproximacion)/2.0 if abs(aproximacion - mejor) < 0.001: return mejor aproximacion = mejor
Si testeamos con estos casos:
print(raiz_newton(2)) print(raiz_newton(5)) print(raiz_newton(9))
El output es:
1.4142135623746899 2.2360679779158037 3.0000000000393214
Se puede mejorar las aproximaciones modificando la condición de stop. También, se puede seguir paso a paso el algoritmo (por ejemplo a mano, o utilizando las herramientas de corrida paso a paso de PyScripter) para ver cuántas iteraciones fueron necesarias para alcanzar las respuestas obtenidas. (tareas para el estudiante)
7.24) Algoritmos
El método de Newton es un ejemplo de algoritmo. Es un proceso mecánico que permite resolver toda una categoría de problemas (en este caso, computar raíces cuadradas).
Algunos tipos de conocimiento no son algorítmicos. Por ejemplo, aprender fechas históricas o las tablas de multiplicar requiere la memorización de soluciones específicas.
Pero las técnicas que aprendiste de cómo sumar (diciendo "me llevo 1") o restar ("pido 1"), o dividir ("me sobran 3 y bajo el 7") son algoritmos. Si sueles jugar al Sudoku, es posible que haya una serie de pasos que sigues habitualmente.
Una de las características de los algoritmos es que no requieren de inteligencia alguna para ser llevados a cabo. Son procesos mecánicos en los cuales cada paso sigue al anterior según reglas simples y estrictas. Y están diseñados para resolver una clase general de problemas, no un problema en particular.
Comprender que problemas incluso muy difíciles pueden ser resueltos con procesos algorítmicos paso a paso (y que tenemos tecnología que puede ejecutar esos pasos por nosotros) ha sido una de las causas principales (si no la causa principal) de los grandes beneficios materiales que ha recibido la sociedad moderna. Por lo tanto, si bien la ejecución de un algoritmo puede ser aburrida y no requerir inteligencia, el pensamiento algorítmico y computacional (i.e. usar algoritmos y automatización como la base para resolver problemas) ha transformado rápidamente a nuestra sociedad. Algunos sostienen que este cambio hacia unas formas de procesos y pensamiento algorítmicos tendrán más impacto en nuestra sociedad que el que tuvo la imprenta hace 500 años. Y el proceso de diseñar los algoritmos es interesante, una fuente de retos intelectuales y una parte fundamental de lo que llamamos programar.
Muchas de las cosas que la gente hace habitualmente, sin dificultad o sin pensarlo conscientemente, son las más difíciles de expresar algorítmicamente. Comprender el lenguaje natural es un buen ejemplo. Todos lo hacemos, pero hasta ahora nadie fue capaz de explicar cómo lo hacemos, al menos no bajo la forma de un algoritmo paso a paso.
- (1) Tal vez porque el proceso sí es algorítmico pero no tiene que ver sólo con palabras, sino con lo que vemos y escuchamos que hace la gente cuando esas palabras están en el aire, y sin esa interacción, que las computadoras no han tenido nunca, a todo algoritmo que implementemos le falta una pata.
- (2) Tal vez porque el proceso no se puede describir como un mecanismo paso a paso, por más que sí se podría comprender o reproducir.
- (3) Tal vez porque el proceso es espiritual, no material, y no hay "mecanismo" que lo pueda describir.
7.25) Glosario
- algoritmo, cuerpo (body), breakpoint, incremento (bump, golpe), decremento, sentencia continue, contador, cursor, iteración, iteración definida, iteración indefinida, plan de desarrollo
- encapsular, generalizar, secuencia de escape (un carácter de escape, \, seguido de uno o más caracteres imprimibles que designan un carácter no imprimible)
- inicialización (de una variable) (en Python es forzoso inicializar una variable al crearla - en otros lenguajes se permite que las variables se creen en un punto y sean inicializadas más adelante)
- (consecuencia: en esos otros lenguajes, entre la creación y la inicialización de la variable ésta contendrá valores por defecto o valores garbage)
- loop, loop infinito, variable del loop, loop mid-test, loop anidado, loop post-test, loop pre-test, ejecución de un paso (single-step)
- meta-notación (vimos en este capítulo algunos casos: corchetes, puntos suspensivos, cursiva y negrita para describir partes opcionales, repetibles, sustituibles y fijas del código)
- carácter de nueva línea, carácter tab, tricotomía, ejecución paso a paso, rastrear (trace)
7.26) Ejercicios
Vimos en este capítulo cómo sumar una lista de items, y cómo contarlos. El ejemplo de la cuenta tenía también una sentencia if que nos permitió contar sólo a algunos de esos elementos. En el capítulo anterior habíamos visto la función encontrar_primer_palabra_de_dos_letras que nos permitió realizar una "salida temprana" del loop mediante la ejecución de un return cuando se dio cierta condición. En este capítulo vimos que también podemos utilizar un break para salir del loop (sin salir de la función que lo contiene) y un continue para abandonar la iteración actual del loop y seguir de inmediato con la próxima.
La combinación de recorrido, suma, conteo, testeo de condiciones y salida rápida de una lista es una rica combinación de bloques elementales que podemos combinar en múltiples formas para crear funciones de todo tipo.
Los 6 primeros ejercicios son funciones típicas que deberías ser capaz de escribir usando esos bloques de construcción:
1) Escribir una función que cuente cuántos números impares hay en una lista. (hacerlo)
2) Sumar todos los números pares de una lista. (hacerlo)
3) Sumar todos los números negativos de una lista. (hacerlo)
4) Contar cuántas palabras en una lista tienen largo 5. (hacerlo)
5) Sumar todos los elementos de una lista hasta que aparezca el primer número par (sin incluirlo). Escribirle una unidad de testeo. ¿Qué pasa si la lista no contiene un número par? (hacerlo)
6) Contar cuántas palabras hay en una lista hasta la primera ocurrencia de la palabra "sam" (la cual incluimos en la cuenta). Escribrrle también una unidad de testeo. ¿Qué pasa si sam no aparece en la lista? (hacerlo)
7) Agregarle una función print a raiz_newton que imprima mejor cada vez que es calculado. Llamar la función así modificada con el valor 25 y observar los resultados. (hacerlo)
8) Rastrea la ejecución de la última versión de tabla_multiplicar (la versión de dos parámetros que se usa en la tablas_multiplicar triangular) y trata de comprender cómo funciona. (hacerlo)
9) Escribir una función numeros_triangulares que imprima los primeros n números triangulares. Un llamado a numeros_triangulares(5) debería producir el siguiente output: (hacerlo)
1 1 2 3 3 6 4 10 5 15
- Pista: busca en la web qué significa "número triangular"
10) Escribe una función es_primo que tome un argumento entero y retorne True si es un número primo y False en caso contrario. Agregar testeos para casos como estos: (hacerlo)
test(is_prime(11)) test(not is_prime(35)) test(is_prime(19911121))
- El último caso debería representar tu fecha de nacimiento. ¿Naciste en un día primo? En una clase de 100 estudiantes, cuántos crees que deberían pasar este test? (hacerlo)
11) Revisa el problema del pirata borracho que vimos en el capítulo 3. (problemas 7 y 8 del capítulo 3). Esta vez, el pirata borracho hace un giro, luego da algunos pasos adelante, y repite esto. Nuestra estudiante de ciencias sociales anota entonces pares de valores: el ángulo de cada giro, y la cantidad de pasos tras el giro. Sus datos experimentales son [(160, 20), (-43, 10), (270, 8), (-43, 12)]. Utiliza una tortuga para dibujar el camino de nuestro amigo borracho. (hacerlo)
12) Muchas formas interesantes pueden ser dibujadas por la tortuga si le pasamos una lista de pares como vimos arriba, en que el primer ítem del par es el ángulo de giro y el segundo es la distancia que ha de avanzar. Define una lista de pares para que la tortuga dibuje una casa con una X en el centro, como se muestra aquí. Debería hacerse sin volver a pasar por ninguna línea ya dibujada, y sin levantar el lápiz. (hacerlo)

- Pistas: puede convenir que lo resuelvas primero con lápiz y papel. También, piensa cuáles son los ángulos en las diagonales y el techo, y cuál es la relación de tamaño entre lados y diagonales.
13) No todas las figuras como la anterior pueden dibujarse sin levantar el lápiz (o sin pasar dos veces por el mismo lado). ¿Cuáles de las siguientes son posibles?

- Respuesta: sí, sí, no, sí, sí, no (las que no son posibles, por tener más de dos vértices con cantidad impar de aristas incidentes)
Ahora lee en wikipedia el artículo Camino euleriano.
- Aprenderás cómo saber de inmediato (con una inspección algorítmica) si es posible o no encontrar una solución.
- Si el camino es posible, sabrás también dónde hay que poner el lápiz para comenzar el camino, y dónde deberías terminar)
14) Qué retornará cantidad_digitos(0)? Modifícalo para que retorne 1 en este caso. ¿Por qué un llamado a cantidad_digitos(-24) queda en loop infinito? (pista: -1 // 10 evalúa a -1). Modifica la función para que funcione bien con números negativos. Agrega estos tests: (hacerlo)
test(cantidad_digitos(0) == 1) test(cantidad_digitos(-12345) == 5)
15) Escribe una función cantidad_digitos_pares(n) que cuente cuántos dígitos pares tiene un número n. Debería pasar estos tests: (hacerlo)
test(cantidad_digitos_pares(123456) == 3) test(cantidad_digitos_pares(2468) == 4) test(cantidad_digitos_pares(1357) == 0) test(cantidad_digitos_pares(0) == 1)
16) Escribe una función suma_de_cuadrados(xs) que compute la suma de los cuadrados de los números de la lista xs. Por ejemplo, suma_de_cuadrados([2, 3, 4]) debería devolver 29 = 4 + 9 + 16.
- Probarla con los siguientes tests:
test(suma_de_cuadrados([2, 3, 4]) == 29) test(suma_de_cuadrados([ ]) == 0) test(suma_de_cuadrados([2, -3, 4]) == 29)
17) Junto con un amigo vas a escribir un juego de Ta-te-tí (Tres en raya) para ser jugado humano vs. computadora. Tu amigo escribirá la lógica para jugar una ronda del juego, mientras que tú escribirás la lógica que permite jugar varias rondas, guardar el score, decidir quién es el que juega en el próximo turno, etc. Ambos tienen que negociar cómo encajará una parte con la otra, y acuerdan este esbozo de "jugar un turno", que tu amigo deberá completar más adelante: (hacer el ejercicio completo - y de paso traducir este código al español)
# Your friend will complete this function
def play_once(human_plays_first):
"""
Must play one round of the game. If the parameter
is True, the human gets to play first, else the
computer gets to play first. When the round ends,
the return value of the function is one of
-1 (human wins), 0 (game drawn), 1 (computer wins).
"""
# This is all dummy scaffolding code right at the moment...
import random # See Modules chapter ...
rng = random.Random()
# Pick a random result between -1 and 1.
result = rng.randrange(-1,2)
print("Human plays first={0}, winner={1} "
.format(human_plays_first, result))
return result- a) Escribe el programa que llama varias veces a esta función para jugar el juego, y tras cada ronda anuncie el resultado como "Gané!", "Ganaste!" o "Empate!". Luego pregunta al jugador: "¿Quieres jugar de nuevo?" y o bien juega de nuevo, o bien dice "Adiós" y termina.
- b) Lleva la cuenta de cuántos partidos ganó cada jugador, y de cuántos empates hubieron. Luego de cada ronda, anuncia el score.
- c) Agrega la lógica necesaria para que los jugadores comiencen el partido alternadamente (un partido comienza uno, otro partido comienza el otro, etc.)
- d) Computa el porcentaje de triunfos de la persona, de entre todos los juegos que jugó. También anúncialo al final de cada ronda.
- e) Dibuja un diagrama de flujo de tu lógica.