Cap. 5 - Condicionales

Los programas se vuelven interesantes cuando chequeamos condiciones y modificamos el comportamiento del programa según el resultado. Ese es el tema central de este capítulo.

5.1) Valores y expresiones booleanos

Un valor booleano es o bien verdadero o bien falso. Se llama así en honor del matemático británico George Boole, quien fuera el primero en formular el álgebra booleana (reglas que permiten razonar con estos valores y combinarlos). Estas reglas son la base de toda la lógica computacional moderna.

En Python, los dos valores booleanos son True y False (deben escribirse exactamente así, con la "T" y "F" mayúscula y el resto en minúsculas). El tipo correspondiente se llama bool.

		>>> type(True)
		
		>>> type(true)
		Traceback (most recent call last):
		  File "", line 1, in 
		NameError: name 'true' is not defined

Una expresión booleana es una expresión al evaluarse produce un valor booleano. Por ejemplo, el operador == chequea si dos valores son iguales, y devuelve un booleano.

		>>> 5 == (3 + 2)   # ¿es cinco igual al resultado de 3 + 2?
		True
		>>> (5 == 5) + 2   # sumarle 2 a True - devuelve 3		(si se le suma a False, devuelve 2; o sea que True se considera un 1 y False se considera un 0 en operaciones numéricas)
		3
		>>> 5 == 6
		False
		>>> j = "hel"
		>>> j + "lo" == "hello"
		True

En los casos en que la igualdad es correcta se retorna True, en caso contrario se retorna False.

El operador == es uno de los 6 operadores de comparación comunes que producen un resultado booleano. La lista completa es:

		x == y               # Produce True si ... x es igual a y
		x != y               # ... x no es igual a y
		x > y                # ... x es mayor que y (estrictamente)
		x < y                # ... x es menor que y (estrictamente)
		x >= y               # ... x es mayor o igual que y
		x <= y               # ... x es menor o igual que y

Si bien las operaciones son conocidas de la matemática, los símbolos que utiliza Python son similares, pero no iguales, a los de aquélla. Evitar el error común de utilizar un sólo signo de igual (=) en vez del doble igual (==). Recordar que el = es un operador de asignación y que el == es un operador de comparación. Por otro lado, no existen operadores como =< o =>

Como los demás tipos que hemos visto, los valores booleanos pueden asignarse a variables, imprimirse, etc.

		>>> edad = 18
		>>> con_suficiente_edad_como_para_manejar = edad >= 17
		>>> print(con_suficiente_edad_como_para_manejar)
		True
		>>> type(con_suficiente_edad_como_para_manejar)
		<class 'bool'>

Observar en la línea 2 cómo a la variable con_suficiente_edad_como_para_manejar se le asigna un booleano (True o False) al asignársele la comparación edad >= 17. En este caso se le asigna True. Si más adelante alguien cambia la edad a 15, la variable con_suficiente_edad_como_para_manejar seguirá siendo True (pues así había sido evaluada). Habría que volver a asignarle edad >= 17 para que ahora guarde un False.

5.2) Operadores lógicos

Hay 3 operadores lógicos and, or y not, que nos permiten construir expresiones booleanas más complejas a partir de otras simples. La semántica (significado) de esos operadores es el mismo que el habitual en inglés.

Ejemplos:

La expresión a la izquierda de un or se evalúa primero. Si da True, Python ya no evalúa la de la derecha (pues no es necesario hacerlo para saber que el resultado global es True). Esto se llama evaluación de cortocircuito (o evaluación de circuito corto). Del mismo modo, para el operador and, si la expresión de la izquierda da False, Python ya no evalúa la expresión de la derecha porque sabe que el global dará False.

Es decir que no se realizan evaluaciones innecesarias.

5.3) Tablas de verdad

Una tabla de verdad es una pequeña tabla que nos permite listar todas las posibles entradas y resultados de un operador lógico. Como los operadores and y or tienen ambos dos operandos, hay 4 filas en sus respectivas tablas de verdad.

Tabla de verdad para el operador and:

		   a		    b		a and b
		False		False		  False
		False		True		  False
		True		False		  False
		True		True		  True

Para no escribir True y False cada vez, podemos abreviar utilizando T y F, o V y F en español.

Tabla de verdad para el operador or:

		   a		    b		a or b
	 	   F		    F		     F
	 	   F		    T		     T
	 	   T		    F		     T
	 	   T		    T		     T

Como el operador or sólo tiene un operando, su tabla de verdad tendrá sólo dos filas:

		   a		not a
	 	   F		    T	
	 	   T		    F

5.4) Simplificando expresiones booleanas

Se llama álgebra a cualquier conjunto de reglas que permitan simplificar y reorganizar expresiones. Por ejemplo, todos conocemos las reglas del álgebra matemática, del tipo:

		n * 0	== 	0

Ahora veremos otra, que es el álgebra booleana, que da reglas para trabajar con valores booleanos.

Primero, reglas para el operador and:

		x   and   False   ==   False
		False   and   x   ==  False
		y and x == x and y
		x and True == x
		True and x == True
		x and x == x

Estas son las reglas correspondientes para el operador or:

		x or False == x
		False or x == x
		y or x == x or y
		x or True == True
		True or x == True
		x or x == x

Dos operadores not se cancelan mutuamente:

		not (not x) == x

5.5) Ejecución condicional

Para escribir programas útiles, casi siempre necesitamos chequear condiciones y cambiar el comportamiento del programa según ellas. Los enunciados condicionales nos permiten hacer esto. El más sencillo es el enunciado if, por ejemplo: (L5_if_else.py)

if x % 2 == 0:
    print(x, " es par ")
    print("Sabías que 2 es el único número par que es primo?")
else:
    print(x, " es impar ")
    print("Sabías que multiplicando dos números impares " +
                "se obtiene siempre un número impar?")

Observación: este programa es interesante, también, porque muestra algunas formas habituales de utilizar la función print.

La expresión booleana tras el if se llama condición. Si es verdadera, entonces todos los enunciados indentados que la siguen son ejecutados. De lo contrario, todos los enunciados indentados tras el else son ejecutados.

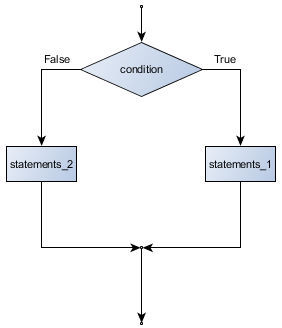
La sintaxis de un enunciado if se ve así:

		if EXPRESIÓN_BOOLEANA:
			SENTENCIAS_1		# Ejecutadas si la expresión booleana evalúa a True
		else:
			SENTENCIAS_2		# Ejecutadas si la expresión booleana evalúa a False

Como con la definición de función del capítulo anterior, o la de otras sentencias compuestas como for, vista antes, el enunciado if tiene un header y un cuerpo. La línea header comienza con la palabra clave if, seguida de una expresión booleana y termina con dos puntos. Las sentencias indentadas que vienen a continuación se llaman bloque. El primer enunciado no indentado señala el final del bloque.

Cada uno de los enunciados dentro del primer bloque se ejecutan en orden si la expresión booleana evalúa a True. Si en cambio evalúa a False, todo el bloque inicial es saltado y se ejecutan en su lugar las sentencias que están en el bloque que sigue a la línea else.

No hay límite a la cantidad de sentencias que se pueden poner en cada bloque, pero tiene que haber al menos una sentencia en cada bloque. De vez en cuando es práctico poder tener un bloque vacío (sin sentencias), por ejemplo como un lugar "a rellenar más adelante" si estamos en el proceso de ir escribiendo el código. En tal caso se puede utilizar la sentencia pass, que no hace nada (sólo actúa como un placeholder).

		if True:			# Esto siempre es True
			pass		# 	así que esto siempre se ejecuta, pero no hace nada
		else:
			pass

5.6) Omitiendo la cláusula ELSE

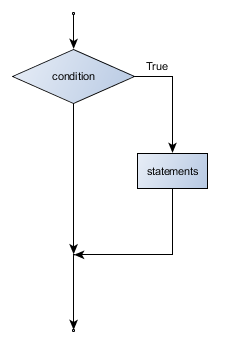
Otra forma del enunciado if es aquella en que la cláusula else se omite por completo. En este caso, cuando el enunciado evalúa a True se ejecutan las sentencias del bloque, y en caso contrario el flujo de ejecución continúa en la línea posterior al if (la primera línea no indentada posterior al bloque). (L5_if_only.py)

import math

x = -3

if x < 0:
    print("El número negativo ", x, " no es válido aquí.")
    x = 49
    print("Decidí usar el número 49 en su lugar.")

print("La raíz cuadrada de ", x, " es ", math.sqrt(x))

En este caso, la función print que muestra la raíz cuadrada está después de la sentencia if (ya que es la primera no indentada después del bloque del if). El llamado a math.sqrt requiere haber importado previamente el módulo math.

Terminología Python: en la documentación de Python a veces se llama suite (sucesión) de sentencias a lo que aquí hemos llamado bloque. Significan lo mismo, pero como en otros lenguajes y en la teoría de la computación en general se suele utilizar el término bloque, lo preferimos antes que el de uso más restringido.

Es importante observar además que else no es una sentencia, sino que es una cláusula que es parte de la sentencia if (la cual puede o no contener a la cláusula else)

5.7) Condicionales encadenados

A veces hay más de dos opciones y necesitamos más ramas. Una forma de conseguirlo es mediante condicionales encadenados:

		if x < y:
			SENTENCIAS_A
		elif x > y:
			SENTENCIAS_B
		else:
			SENTENCIAS_C

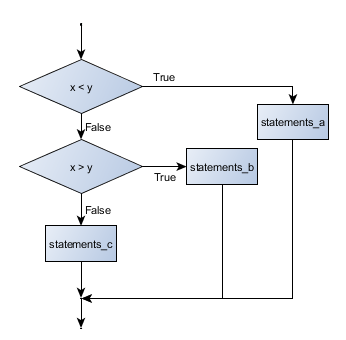
elif es una abrevaición de else if. Como antes, sólo una de las ramas será ejecutada (la primera cuya condición se cumpla). No hay límite a cuántos elif se pueden poner pero sólo se permite un else (opcional) final y debe ser la última cláusula de la sentencia.

if choice == "a":
    function_one()
elif choice == "b":
    function_two()
elif choice == "c":
    function_three()
else:
    print("Invalid choice.")

Cada condición se chequea en orden. Si la primera es falsa, la próxima es chequeada, y así sucesivamente. Si una es verdadera, el correspondiente bloque se ejecuta, y la sentencia termina. Incluso si más de una condición es verdadera, sólo se ejecuta el bloque de la primera rama verdadera.

5.8) Condicionales anidados

Se puede anidar también a un condicional dentro de otro (viene a ser un caso más de composición). Podríamos haber escrito el ejemplo anterior así:

		if x < y:
		    STATEMENTS_A
		else:
		    if x > y:
		        STATEMENTS_B
		    else:
		        STATEMENTS_C

El condicional externo contiene 2 ramas. La segunda rama contiene otra sentencia if, que tiene sus propias dos ramas. Esas dos ramas podrían a su vez haber contenido más condicionales.

A pesar de que la indentación de los condicionales facilita la comprensión, muchos condicionales anidados son difíciles de leer. En general es buena idea evitarlos tanto como sea posible.

Los operadores lógicos proveen habitualmente una forma de simplificar sentencias condicionales. Por ejemplo, podemos reescribir el siguiente código con un único condicional:

		if 0 < x:            # Suponemos aquí que x es un entero
		    if x < 10:
		        print("x es un entero positivo y tiene un único dígito.")

La función print sólo se llama si dieron True las dos condiciones. Por lo tanto, podríamos utilizar el operador and para lograr exactamente el mismo efecto, con un solo condicional:

		if 0 < x and x < 10:            # Suponemos aquí que x es un entero
		    print("x es un entero positivo y tiene un único dígito.")

5.9) La sentencia RETURN

La sentencia return (con o sin valor, según que la función sea o no fructífera) permite interrumpir la ejecución de una función antes de que llegue al final.

Una razón típica para un retorno temprano es haber detectado una condición de error. (L5_if_return.py)

def mostrar_raiz_cuadrada(x):
    if x < 0:
        print("Sólo números positivos, por favor")
        return

    raiz = x**0.5
    print("La raíz cuadrada de ", x, " es ", raiz)

La función mostrar_raiz_cuadrada tiene un parámetro x. Lo primero que hace es chequear si x es negativo, en cuyo caso muestra un mensaje de error y la función retorna. El flujo de ejecución vuelve de inmediato al caller, y el resto de la función no se ejecuta.

5.10) Opuestos lógicos

Cada uno de los 6 operadores relacionales tiene un opuesto lógico. Por ejemplo, si podemos obtener la licencia de conducir a una edad mayor o igual a 17, quiere decir que no la podemos obtener a una edad menor que 17. Es decir, el opuesto de >= es <

	     operador		   opuesto lógico
	       ==			!=
	       !=			==
	       <			>=
	       <=			>
	       >			<=
	       >=			<

Comprender bien estos opuestos lógicos nos puede ahorrar el uso de varios not. Los operadores not suelen ser difíciles de leer cuando el código se complica, y será más fácil de comprender qué intentábamos hacer si evitamos usarlos.

Por ejemplo, podemos escribir esto en Python:

	if not (edad >= 17):
	    print("Eres demasiado joven para tener una licencia!")

Pero es más claro utilizar la siguiente simplificación:

	if edad < 17:
	    print("Eres demasiado joven para tener una licencia!")

Dos leyes de simplificación poderosas, conocidas como leyes de de Morgan son útiles cuando trabajamos con expresiones lógicas complicadas:

	not (x and y)  ==  (not x) or (not y)
	not (x or y)   ==  (not x) and (not y)

Por ejemplo, supongamos que sólo se puede matar al dragón si nuestra espada mágica está cargada con 90% o más de poder, y tenemos 100 o más unidades de poder en nuestro escudo protector. Encontraríamos un fragmento de código así en el programa correspondiente:

	if not ((sword_charge >= 0.90) and (shield_energy >= 100)):
	    print("Tu ataque no tiene efecto, el dragón te rostizó!")
	else:
	    print("El dragón se hunde en el abismo. Has rescatado a la bella princesa!")

Las leyes de de Morgan junto con el uso de opuestos lógicos nos permiten escribir la condición de un modo más comprensible, así:

	if (sword_charge < 0.90) or (shield_energy < 100):
	    print("Tu ataque no tiene efecto, el dragón te rostizó!")
	else:
	    print("El dragón se hunde en el abismo. Has rescatado a la bella princesa!")

También podríamos haber eliminado el not de la primera versión invirtiendo el orden de los bloques if y else, así:

	if (sword_charge >= 0.90) and (shield_energy >= 100):
	    print("El dragón se hunde en el abismo. Has rescatado a la bella princesa!")
	else:
	    print("Tu ataque no tiene efecto, el dragón te rostizó!")

Tal vez esta última versión sea la mejor de las tres, porque es la que más se parece a como la diríamos hablando en lenguaje humano (en español o inglés). La claridad de nuestro código (para otros humanos) en el sentido de facilitar la comprensión de qué es lo que hace el código debería ser siempre de gran prioridad.

A medida que desarrollemos nuestras habilidades de programación comenzaremos a ver que hay varias formas de resolver el mismo problema. Por lo tanto, los buenos programas comienzan por un buen diseño. Llevamos a cabo elecciones que favorecen (o no) una mayor claridad, simplicidad y elegancia. El título arquitecto de software dice muchísimo sobre lo que hacemos: somos arquitectos que desarrollan sus productos buscando un balance entre belleza, funcionalidad, simplicidad y claridad en nuestras creaciones.

Tip: Cuando un programa ya funciona, deberíamos probarlo e irlo puliendo. Escribir buenos comentarios. Pensar dónde podría quedar más claro usando otra clase de nombres de variables y funciones. ¿Se podría hacer de un modo más sencillo? ¿Deberíamos usar más funciones? ¿Podemos simplificar los condicionales? Vemos nuestro código como una creación y una obra de arte, y buscamos mejorarlo en cada detalle.

5.11) Conversión de tipos

Ya hablamos de esto en algún capítulo anterior. Muchos tipos de Python vienen con funciones built-in que permiten convertir sus valores a otros tipos. La función int, por ejemplo, toma cualquier valor y lo convierte a un entero, si es posible, o bien emite un mensaje de error explicando que no es posible:

		>>> int("32")
		32
		>>> int("Hello")
		ValueError: invalid literal for int() with base 10: 'Hello'

También int permite convertir números float (decimales) a enteros, pero recordemos que lo que hace es truncar la parte decimal:

		>>> int(-2.3)
		-2
		>>> int(3.99999)
		3
		>>> int("42")
		42
		>>> int(1.0)
		1

La función float convierte enteros y strings a floats:

		>>> float(32)
		32.0
		>>> float("3.14159")
		3.14159
		>>> float(1)
		1.0
		>>> float("hola")
		Traceback (most recent call last):
		  File "<interactive input>", line 1, in <module>
		ValueError: could not convert string to float: 'hola'

Podría parecer extraño que Python haga distinción entre el valor 1 entero y el valor 1.0 float. Es cierto que representan el mismo número, pero pertenecen a distintos tipos. Es importante no confundirlos porque su representación interna es diferente (a nivel de la computadora).

La función str convierte a cualquier argumento al tipo string:

		>>> str(32)
		'32'
		>>> str(3.14149)
		'3.14149'
		>>> str(True)
		'True'
		>>> str(true)
		Traceback (most recent call last):
		  File "<interactive input>", line 1, in 
		NameError: name 'true' is not defined

Esta función convierte cualquier valor a un string. Como vimos antes, True es un valor booleano, pero true es un nombre de variable ordinario, y como no ha sido definido en un paso previo, devuelve un mensaje de error.

5.12) Un diagrama de barras con tortugas

Con la tortuga se pueden hacer muchas más cosas que las que vimos hasta ahora. La documentación completa sobre el módulo turtle se puede encontrar en http://docs.python.org/py3k/library/turtle.html, o en PyScripter, buscando "turtle" en la Ayuda.

Aquí tenemos un par de trucos nuevos para la tortuga:

Con todo lo anterior, hagamos que tess dibuje un diagrama de barras. Comencemos con una lista de valores a graficar:

		xs = [48, 117, 200, 240, 160, 260, 220]

Dibujaremos rectángulos cuyas alturas correspondan a los datos anteriores y cuyos anchos sean del mismo valor: (L5_bar_chart.py)

import turtle

def dibujar_barra(t, alto):
    """ Hacer que la tortuga t dibuje un rectángulo de altura alto."""

    t.left(90)
    t.forward(alto)       # Dibuja el lado izquierdo del rectángulo
    t.right(90)
    t.forward(40)           # Dibuja el ancho por el lado de arriba
    t.right(90)
    t.forward(alto)       # Dibuja el lado derecho
    t.left(90)              # Hacer que la tortuga mire para el lugar hacia donde miraba inicialmente
    t.forward(10)           # Dejar una pequeña distancia entre barra y barra

wn = turtle.Screen()        #Setear la ventana
wn.bgcolor("lightgreen")

tess = turtle.Turtle()      #Crear a tess y setear algunos atributos
tess.color("blue")
tess.pensize(3)

tess.left(180)              # Moverse hacia la izquierda antes de empezar a dibujar
tess.forward(150)
tess.left(180)

xs = [48, 117, 200, 240, 160, 260, 220]
for v in xs:
    dibujar_barra(tess, v)

wn.mainloop()

Se obtiene algo así:

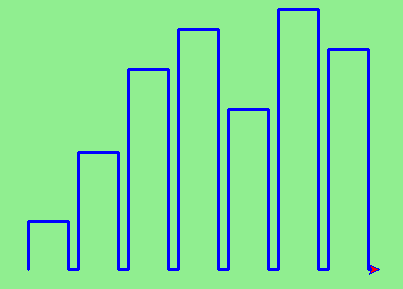
No muy impresionante, pero es un buen comienzo. Lo importante aquí fue que pudimos subdividir el problema en etapas: en cada etapa dibujamos una barra, y lo hacemos a través de una función que escribimos específicamente para conseguir esto. Luego, para dibujar todo el diagrama, llamamos varias veces (7 veces) a esta función.

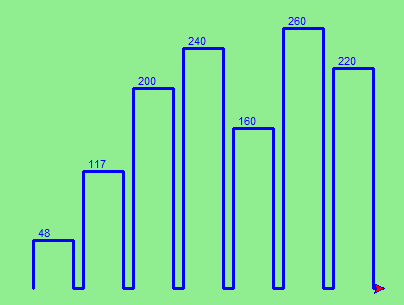
Ahora, en el top de cada barra queremos imprimir el valor numérico correspondiente al dato de la misma.

Lo haremos mediante una línea t.write(' ' + str(alto)) justo antes de dibujar el "techo" de la barra, en la función dibujar_barra. Dejamos un pequeño espacio adelante del número para que se vea centrado. También convertimos el número en un string mediante la función str. El resultado se ve más o menos así:

Lo siguiente es que queremos rellenar las barras con un color, para lo cual modificamos la línea que setea el color, para que sea así: tess.color("blue", "red"). Y además agregamos llamados a t.begin_fill() y t.end_fill() en las líneas adecuadas del código de la función, obteniendo este código final: (L5_bar_chart_relleno.py)

import turtle

def dibujar_barra(t, alto):
    """ Hacer que la tortuga t dibuje un rectángulo de altura alto."""

    t.begin_fill()        # Esta línea indica que vamos a rellenar
    t.left(90)
    t.forward(alto)       # Dibuja el lado izquierdo del rectángulo
    t.write('   ' + str(alto))
    t.right(90)
    t.forward(40)           # Dibuja el ancho por el lado de arriba
    t.right(90)
    t.forward(alto)       # Dibuja el lado derecho
    t.left(90)              # Hacer que la tortuga mire para el lugar hacia donde miraba inicialmente
    t.end_fill()            #Esta línea indica que rellenamos hasta acá
    t.forward(10)           # Dejar una pequeña distancia entre barra y barra

wn = turtle.Screen()        #Setear la ventana
wn.bgcolor("lightgreen")

tess = turtle.Turtle()      #Crear a tess y setear algunos atributos
tess.color("blue", "red")
tess.pensize(3)

tess.left(180)              # Moverse hacia la izquierda antes de empezar a dibujar
tess.forward(150)
tess.left(180)

xs = [48, 117, 200, 240, 160, 260, 220]
for v in xs:
    dibujar_barra(tess, v)

wn.mainloop()

Lo que produce el siguiente gráfico:

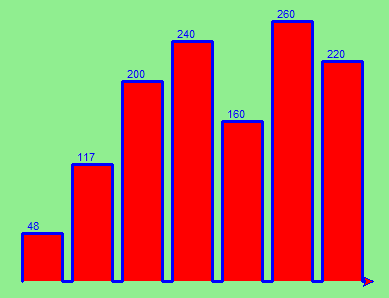
Mejoró mucho. Todavía se podría mejorar eliminando la línea inicial y la conexión horizontal entre las barras en el piso. Esto se haría levantando el lápiz entre barra y barra, y lo dejamos como ejercicio.

5.13) Glosario

5.14) Ejercicios

1) Suponer que los días de la semana están numerados 1, 2, 3, 4, 5, 6, 7 de Domingo a Sábado. Escribir una función que dado el número del día, devuelva su nombre (un string). (hacerlo)

 

2) Te vas de vacaciones un día 3 (miércoles). Volvés a casa después de dormir 137 noches. Escribir una función general que pida al usuario cuál es el día inicial y el largo de la estadía, y devuelva el nombre del día de la semana en que estarás volviendo. (hacerlo)

 

3) Dar los opuestos lógicos de estas condiciones

1) a > b		2) a >= b	3) a >= 18 and day == 3		4) a >= 18 and day != 3

 

4) A qué evalúan estas expresiones?

1) 3 == 3	2) 3 != 3		3) 3 >= 4	4) not (3 < 4)

 

5) Completar esta tabla de verdad:

		p	q	r		(not(p and q)) or r
		F	F	F			
		F	F	T			
		F	T	F			
		F	T	T			
		T	F	F			
		T	F	T			
		T	T	F			
		T	T	T

 

6) Escribir una función que recibe un puntaje de examen y devuelve un string (la calificación conceptual correspondiente a dicho puntaje), según el siguiente esquema: (hacerlo)

		Nota		Calificación
		>= 75		Primero
		[70-75)		Segundo Superior
		[60-70)		Segundo
		[50-60)		Tercero
		[45-50)		F1 Superior
		[40-45)		F2
		< 40		F3

 

7) Modificar el programa del diagrama de barras con la tortuga para que las líneas horizontales entre barra y barra ya no se dibujen. (hacerlo)

 

8) Modificar el programa del diagrama de barras para que los valores por encima de 200 se pinten con rojo, los que están entre 100 y 200 con amarillo, y los menores de 100 con verde. (hacerlo)

 

9) En el programa del diagrama de barras, ¿qué pasaría si alguno de los valores de la lista fuera negativo? Cambiar el programa para que el texto se imprima fuera del rectángulo en ese caso. (hacerlo)

 

10) Escribir una función encontrar_hipotenusa que, dados los largos de los dos catetos de un triángulo rectángulo, retorna el largo de la hipotenusa. (hacerlo)

 

11) Escribir una función es_rectángulo que dado el largo de 3 lados de un triángulo determina si el triángulo es o no es rectángulo. Asumir que el tercer parámetro corresponde siempre al lado más largo.

 

12) Extender el programa anterior para que los 3 lados se puedan recibir en cualquier orden (ya no es necesario que el más largo sea el tercero) (hacerlo)

 

13) La razón por la que la aritmética float es inexacta se comprende con facilidad si uno intenta expresar 1/3 en números decimales.