Cap. 18 - Recursión

18.1) Dibujando fractales

Para nuestros propósitos, un fractal es un dibujo que tiene una estructura auto-similar, la cual por partes puede ser definida en términos de sí misma.

Comencemos por el famoso fractal de Koch. Un fractal de Koch de orden 0 es simplemente un segmento de recta de cierto tamaño.

Un fractal de Koch de orden 1 se obtiene así: Dibujar 4 segmentos más pequeños que el anterior, que lo sustituyen, según el siguiente patrón:

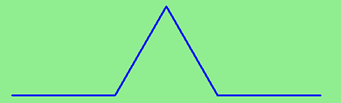
Ahora qué pasaría si aplicáramos este patrón de Koch a cada uno de estos 4 segmentos? Obtendríamos el fractal de Koch de orden 2:

Si repetimos el patrón otra vez, modificando cada segmento, obtenemos el fractal de Koch de orden 3:

Ahora pensemos el asunto marcha atrás. Para dibujar un fractal de Koch de orden 3, alcanza con dibujar 4 fractales de Koch de orden 2. Pero cada uno de éstos a su vez requiere dibujar 4 fractales de Koch de orden 1, y cada uno de éstos requiere dibujar 4 fractales de orden 0. En última instancia, lo último que realmente estaremos dibujando son fractales de orden 0. Esto es muy fácil de programar en Python:

def koch(t, orden, tamaño):
    """
       Haz que la tortuga t dibuje un fractal de Koch de 'orden' y 'tamaño' indicados.
       Dejar a la tortuga apuntando en la dirección original.
    """

    if orden == 0:          # El caso base es sólo una línea recta
        t.forward(tamaño)
    else:
        koch(t, orden-1, tamaño/3)   # Avanzar 1/3 del camino
        t.left(60)
        koch(t, orden-1, tamaño/3)
        t.right(120)
        koch(t, orden-1, tamaño/3)
        t.left(60)
        koch(t, orden-1, tamaño/3)

• Recuerda que para probarlo te alcanza con importar turtle y crear una ventana y una tortuga, así:

import turtle

# (Aquí va el código de la función koch)

wn = turtle.Screen()      # Crea la ventana para las tortugas
t = turtle.Turtle()       # Crea a la tortuga t

koch(t, 3, 243)

wn.mainloop()

La clave para entender el código de la función koch es que si el orden no es cero, koch se llama a sí misma recursivamente para terminar de hacer el trabajo.

Hagamos una observación simple que nos permitirá reducir el código. Recordemos que dar vuelta a la derecha 120° es lo mismo que dar vuelta a la derecha -120°

• Por lo tanto, podemos escribir la parte recursiva del código como un loop for, así:

def koch(t, orden, tamaño):
    if orden == 0:          # El caso base es sólo una línea recta
        t.forward(tamaño)
    else:
        for angulo in [60, -120, 60, 0]:
           koch(t, orden-1, tamaño/3)
           t.left(angulo)

El giro final es de 0°, por lo cual no tiene efecto. Pero nos permitió encontrar un patrón y reducir 7 líneas de código a 3, lo cual hará las cosas más fáciles de comprender en las observaciones que siguen.

def koch_0(t, tamaño):
    t.forward(tamaño)

def koch_1(t, tamaño):
    for angulo in [60, -120, 60, 0]:
       koch_0(t, tamaño/3)
       t.left(angulo)

def koch_2(t, tamaño):
    for angulo in [60, -120, 60, 0]:
       koch_1(t, tamaño/3)
       t.left(angulo)

def koch_3(t, tamaño):
    for angulo in [60, -120, 60, 0]:
       koch_2(t, tamaño/3)
       t.left(angulo)

18.2) Estructuras de datos recursivos

Todos los tipos de datos de Python que hemos visto pueden agruparse en listas y tuplas en muchas formas. Las listas y tuplas a su vez pueden estar anidadas, lo que nos da muchas posibles formas de organizar datos. La organización de datos con el propósito de hacer más fácil su uso se llama estructura de datos.

Es tiempo de elecciones y queremos computar los votos a medida que van llegando. Los votos que van llegando de distintos circuitos, en localidades, ciudades y la capital suelen reportarse por un lado como una suma del total de votos y en otros casos como una lista de subtotales (por departamento, por partido, por ciudad, urbano o rural, según la edad promedio de los votantes de los circuitos, etc.). Después de considerar cómo es mejor ir guardando los datos, decidimos usar una lista numérica anidada que definimos como sigue:

Una lista numérica anidada es una lista cuyos elementos son de uno de los dos tipos siguientes:

• a. Número
• b. Lista numérica anidada

Observar que el término lista numérica anidada se utiliza en su propia definición. Definiciones recursivas como ésta son muy comunes en matemáticas y ciencia de la computación. Permiten describir de un modo conciso y expresivo estructuras recursivas de datos que se componen parcialmente de instancias más pequeñas y simples de sí mismas. La definición no es circular, ya que en cierto punto alcanzaremos una lista que no tiene ninguna lista como elemento (es decir, no tiene ninguna lista anidada).

Ahora, supongamos que queremos escribir una función que va a sumar todos los valores de una lista numérica anidada. Python ya viene con una función built-in que devuelve la suma de una secuencia de números:

>>> sum([1, 2, 8])
11

Pero para nuestra lista numérica anidada, la función sum no va a funcionar:

>>> sum([1, 2, [11, 13], 8])
Traceback (most recent call last):
  File "", line 1, in 
TypeError: unsupported operand type(s) for +: 'int' and 'list'

El problema es que el tercer elemento de esta lista, [11, 13], no es un número sino una lista, y por lo tanto no puede ser sumado a los otros 3 elementos 1, 2 y 8.

18.3) Procesando listas numéricas recursivas

Para sumar todos los números en nuestra lista numérica anidada recursivamente deberemos recorrer la lista, visitando cada uno de los elementos que están dentro de su estructura anidada, sumando cada elemento numérico que encontremos y repitiendo recursivamente el proceso de la suma con todos los elementos que sean sub-listas.

Gracias a la recursión, el código Python necesario para sumar los números de una lista numérica anidada es realmente corto:

def suma_recursiva(lista_numerica_anidada):
    total = 0
    for elemento in lista_numerica_anidada:
        if type(elemento) == type([]):
            total += suma_recursiva(elemento)
        else:
            total += elemento
    return total

El body de suma_recursiva consiste principalmente en un for loop que recorre la lista_numerica_anidada.

• Si elemento es un valor numérico (la rama else), simplemente lo sumamos a total.
• Si elemento es una lista, entonces llamamos a suma_recursiva otra vez, con el elemento como argumento.

La sentencia dentro de la función en que ésta se llama a sí misma se conoce como la llamada recursiva.

• El ejemplo anterior tiene un caso base (la rama else) que no conduce a un llamado recursivo: el caso en que el elemento no es una sublista.
• Sin un caso base, tendríamos recursión infinita y el programa no funcionaría (de hecho nunca terminaría de ejecutar).

La recursión es ciertamente una de las herramientas más elegantes y poderosas en la ciencia de la computación.

Un problema un poco más complicado es encontrar el número más grande en nuestra lista numérica anidada:

def r_max(lista_anidada):
    """
      Encontrar el máximo en una estructura recursiva de listas.
      Precondición: Ninguna lista o sublista está vacía.
    """
    mayor = None
    primera_vez = True
    for e in lista_anidada:
        if type(e) == type([]):
            val = r_max(e)
        else:
            val = e

        if primera_vez or val > mayor:
            mayor = val
            primera_vez = False

    return mayor

test(r_max([2, 9, [1, 13], 8, 6]) == 13)
test(r_max([2, [[100, 7], 90], [1, 13], 8, 6]) == 100)
test(r_max([[[13, 7], 90], 2, [1, 100], 8, 6]) == 100)
test(r_max(["joe", ["sam", "ben"]]) == "sam")

Se incluyen tests como ejemplos del uso de la función r_max.

La dificultad de este problema era encontrar un valor con el que inicializar a la variable mayor. No podemos utilizar lista_anidada[0], porque dicho elemento podría ser una lista (no podemos estar seguros de antemano de que se trate de un número). La solución es inicializar una flag booleana en cada paso de recursión, que llamamos primera_vez. Cuando hemos encontrado un valor numérico en la lista, chequeamos a ver si es el primer número que encontramos, o bien si es un valor que tenemos que comparar con una versión ya disponible de mayor.

Una vez más tenemos aquí un caso base, que es cuando el elemento de la lista resulta ser un número. Si no diéramos este caso base, Python seguiría buscando recursivamente hasta llegar a un límite interno de niveles de recursión. Se puede chequear esto con un programita como el siguiente:

def recursion_profundidad(num):
    print("{0}, ".format(num), end="")
    recursion_profundidad(num + 1)

recursion_profundidad(0)

Después de una larga ristra de mensajes, veremos al final un largo traceback que termina con un mensaje como este:

RuntimeError: maximum recursion depth exceeded ...

Por cierto no querríamos que nada así le pasara a uno de los usuarios de nuestros programas, así que en el próximo capítulo veremos cómo se manejan errores en Python.

18.4) Caso de estudio: los números de Fibonacci

La famosa secuencia de Fibonacci 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 134, ... fue planteada por Fibonacci (1170-1250), quien la utilizó para modelizar la descendencia de (parejas) de conejos. Si en la generación 7 tienes 21 pares en total, de los cuales 13 son adultos, en la siguiente generación todos los adultos habrán tenido nuevas crías, y sus crías anteriores habrán crecido hasta ser adultos. Así que en la generación 8 tendrás 21 + 13 = 34, de los cuales 21 serán adultos.

Este modelo para describir la proliferación de conejos hace la suposición simplificatoria dde que los conejos no se mueren. Los científicos suelen hacer suposiciones y establecer restricciones simplificatorias (muy poco realistas) para avanzar un poco en su comprensión del problema.

Si enumeramos los términos de la secuencia a partir de 0, podemos describir cada término recursivamente como la suma de los dos anteriores:

fib(0) = 0
fib(1) = 1
fib(n) = fib(n-1) + fib(n-2)	para n >= 2

Esto se traduce muy fácilmente a código Python:

def fib(n):
    if n <= 1:
        return n
    t = fib(n-1) + fib(n-2)
    return t

Este es un algoritmo extremadamente ineficiente, y veremos una forma de mejorarlo cuando aprendamos algo sobre diccionarios.

import time
t0 = time.time()
n = 35
result = fib(n)
t1 = time.time()

print("fib({0}) = {1}, ({2:.2f} secs)".format(n, result, t1-t0))

Vemos el resultado correcto, pero con una cantidad explosiva de trabajo!

fib(35) = 9227465, (12.33 secs)

18.5) Ejemplo con directorios (carpetas) y archivos recursivos

El siguiente programa devuelve la lista de contenidos de un directorio y de todos sus subdirectorios.

import os

def get_directorio_contenido(camino):
    """
      Devuelve una lista ordenada con todos los contenidos (archivos o directorios) bajo path.
      Esto retorna sólo los nombres, no el camino completo a cada elemento.
    """
    lista_directorio = os.listdir(camino)
    lista_directorio.sort()
    return lista_directorio

def print_archivos(camino, prefijo = ""):
    """ Imprime recursivamente la lista de contenidos en camino """
    if prefijo == "":  # Detectar si estamos en el llamado más externo e imprimir encabezado
        print("Lista de carpetas para", camino)
        prefijo = "| "

    lista_directorio = get_directorio_contenido(camino)
    for f in lista_directorio:
        print(prefijo+f)                   # Print de la línea
        nombre_completo = os.path.join(camino, f)   # Convertir el nombre en nombre completo
        if os.path.isdir(nombre_completo):        # If es directorio, llamada recursiva
            print_archivos(nombre_completo, prefijo + "| ")

El llamado a la función print_archivos con algún camino a folder como parámetro producirá un output como el que sigue:

print_archivos("C:\\Users\\javid\\AppData\\Roaming\\Python\\Python310\\site-packages\\pygame\\examples")
Lista de carpetas para C:\Users\javid\AppData\Roaming\Python\Python310\site-packages\pygame\examples
| README.rst
| __init__.py
| __pycache__
| | __init__.cpython-310.pyc
| | aacircle.cpython-310.pyc
| | aliens.cpython-310.pyc
| | arraydemo.cpython-310.pyc
| | audiocapture.cpython-310.pyc
| | blend_fill.cpython-310.pyc
| | blit_blends.cpython-310.pyc
| | camera.cpython-310.pyc
| | chimp.cpython-310.pyc
| | cursors.cpython-310.pyc
| | dropevent.cpython-310.pyc
| | eventlist.cpython-310.pyc
| | font_viewer.cpython-310.pyc
| | fonty.cpython-310.pyc
| | freetype_misc.cpython-310.pyc
| | glcube.cpython-310.pyc
| | headless_no_windows_needed.cpython-310.pyc
| | joystick.cpython-310.pyc
| | liquid.cpython-310.pyc
| | mask.cpython-310.pyc
| | midi.cpython-310.pyc
| | moveit.cpython-310.pyc
| | music_drop_fade.cpython-310.pyc
| | pixelarray.cpython-310.pyc
| | playmus.cpython-310.pyc
| | prevent_display_stretching.cpython-310.pyc
| | resizing_new.cpython-310.pyc
| | scaletest.cpython-310.pyc
| | scrap_clipboard.cpython-310.pyc
| | scroll.cpython-310.pyc
| | setmodescale.cpython-310.pyc
| | sound.cpython-310.pyc
| | sound_array_demos.cpython-310.pyc
| | sprite_texture.cpython-310.pyc
| | stars.cpython-310.pyc
| | testsprite.cpython-310.pyc
| | textinput.cpython-310.pyc
| | vgrade.cpython-310.pyc
| | video.cpython-310.pyc
| aacircle.py
| aliens.py
| arraydemo.py
| audiocapture.py
| blend_fill.py
| blit_blends.py
| camera.py
| chimp.py
| cursors.py
| data
| | BGR.png
| | alien1.gif
| | alien1.jpg
| | alien1.png
| | alien2.gif
| | alien2.png
| | alien3.gif
| | alien3.png
| | arraydemo.bmp
| | asprite.bmp
| | background.gif
| | black.ppm
| | blue.gif
| | blue.mpg
| | bomb.gif
| | boom.wav
| | brick.png
| | car_door.wav
| | chimp.png
| | city.png
| | crimson.pnm
| | danger.gif
| | explosion1.gif
| | fist.png
| | green.pcx
| | grey.pgm
| | house_lo.mp3
| | house_lo.ogg
| | house_lo.wav
| | laplacian.png
| | liquid.bmp
| | midikeys.png
| | player1.gif
| | punch.wav
| | purple.xpm
| | red.jpg
| | sans.ttf
| | scarlet.webp
| | secosmic_lo.wav
| | shot.gif
| | static.png
| | teal.svg
| | turquoise.tif
| | whiff.wav
| | yellow.tga
| dropevent.py
| eventlist.py
| font_viewer.py
| fonty.py
| freetype_misc.py
| glcube.py
| headless_no_windows_needed.py
| joystick.py
| liquid.py
| mask.py
| midi.py
| moveit.py
| music_drop_fade.py
| pixelarray.py
| playmus.py
| prevent_display_stretching.py
| resizing_new.py
| scaletest.py
| scrap_clipboard.py
| scroll.py
| setmodescale.py
| sound.py
| sound_array_demos.py
| sprite_texture.py
| stars.py
| testsprite.py
| textinput.py
| vgrade.py
| video.py

18.6) Glosario

• caso base, recursión, recursión infinita, llamada recursiva, definición recursiva

18.7) Ejercicios

1) Modificar el programa fractal de Koch para que dibuje un copo de nieve de Koch, así: (hacerlo)

2) a. Dibujar un fractal de línea quebrada de Cesaro, del orden dado por el usuario. Mostramos 4 líneas de orden 0, 1, 2 y 3. En este ejemplo, el ángulo de la lágrima es de 10 grados. (hacerlo)

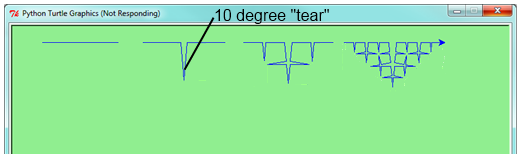
b. Cuatro líneas hacen un cuadrado. Usar el código de la parte (a) para dibujar cuadrados de Cesaro. La variación del ángulo da interesantes efectos - experimentar un poco, o tal vez permitir que el usuario ingrese el ángulo de la lágrima. (hacerlo)

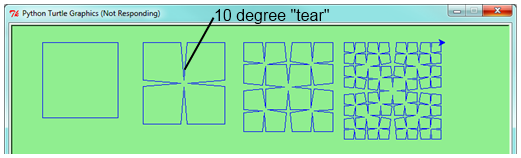
c. (Para los aficionados a las matemáticas). En los cuadrados mostrados aquí, los dibujos de mayor orden se vuelven un poco más grandes (mirar las partes bajas de los cuadrados - no están alineadas). Esto ocurre porque hemos dividido al medio la parte de la línea por cada paso recursivo. Así que hemos "agrandado" el cuadrado total según el tamaño de las bases de las lágrimas. ¿Puedes resolver el problema geométrico para que el tamaño total del subproblema (incluyendo la lágrima) sea igual al tamaño total del original? (hacerlo)

3) Un triángulo de Sierpinski de orden 0 es un triángulo equilátero. Uno de orden 1 se puede dibujar dibujando 3 triángulos menores (que aquí se muestran ligeramente separados, para facilitar la comprensión). Los triángulo de orden mayor, 2 y 3, también se muestran en la figura. Dibuja triángulos de Sierpinski de cualquier orden que sea ingresado por el usuario. (hacerlo)

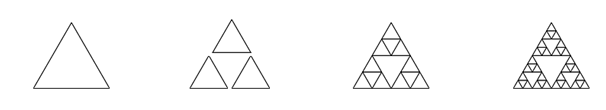
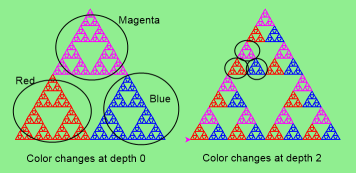
4) Adaptar el programa anterior para cambiar el color de sus tres subtriángulo en cierto nivel de recursión. La ilustración siguiente muestra dos casos: a la izquierda, el color se cambia en el nivel 0 (el nivel más externo de recursión) y en la derecha en el nivel 2. Si el usuario pasa una profundidad negativa, no cambiar el color. (hacerlo)

• Pista: agrega un nuevo parámetro opcional profundidad_cambio_color (con valor por defecto -1) e ir disminuyendo a éste en cada llamada recursiva. Luego en la sección de código que precede a la recursión, verificar si este parámetro es cero, caso en el cual habrá que cambiar de color.

5) Escribir una función, min_recursivo, que retorne el valor más pequeño en una lista numérica anidada. Se puede asumir que no hay listas o sublistas vacías: (hacerlo)

test(min_recursivo([2, 9, [1, 13], 8, 6]) == 1)
test(min_recursivo([2, [[100, 1], 90], [10, 13], 8, 6]) == 1)
test(min_recursivo([2, [[13, -7], 90], [1, 100], 8, 6]) == -7)
test(min_recursivo([[[-13, 7], 90], 2, [1, 100], 8, 6]) == -13)

6) Escribir una función recuento que devuelva la cantidad de ocurrencias de objeto en una lista anidada: (hacerlo)

test(recuento(2, []), 0)
test(recuento(2, [2, 9, [2, 1, 13, 2], 8, [2, 6]]) == 4)
test(recuento(7, [[9, [7, 1, 13, 2], 8], [7, 6]]) == 2)
test(recuento(15, [[9, [7, 1, 13, 2], 8], [2, 6]]) == 0)
test(recuento(5, [[5, [5, [1, 5], 5], 5], [5, 6]]) == 6)
test(recuento("una", [["cosa",["una",["cosa","una"],"una"],"es"], ["una","fácil"]]) == 4)

7) Escribir una función aplanar que retorne una lista simple que contengan todas los valores de una lista anidada (hacerlo)

test(aplanar([2,9,[2,1,13,2],8,[2,6]]) == [2,9,2,1,13,2,8,2,6])
test(aplanar([[9,[7,1,13,2],8],[7,6]]) == [9,7,1,13,2,8,7,6])
test(aplanar([[9,[7,1,13,2],8],[2,6]]) == [9,7,1,13,2,8,2,6])
test(aplanar([["esta",["una",["cosa"],"una"],"es"],["una","fácil"]]) ==
              ["esta","una","cosa","una","es","una","fácil"])
test(aplanar([]) == [])

8) Reescribe el algoritmo de Fibonacci sin usar recursión. ¿Puedes encontrar elementos más grandes de la secuencia? ¿Puedes encontrar fib(200)? (hacerlo)

• Respueta: una implementación secuencial, no recursiva, no crecerá exponencialmente en las operaciones necesarias (como hace la recursiva), sino linealmente, por lo cual será mucho más rápida

9) Usa la ayuda para aprender qué hacen sys.getrecursionlimit() y sys.setrecursionlimit(n). Crea varios experimentos similares al que hicimos con la función recursion_profundidad para testear tu comprensión de cómo funcionan estas funciones del módulo sys. (hacerlo)

10) Escribe un programa que recorra la estructura de un directorio (como en la sección final de este capítulo), pero en vez de imprimir los nombres de archivo, retorne una lista con todos los caminos completos a los archivos en el directorio y subdirectorios. (No incluyas los directorios en la lista - sólo los archivos). Por ejemplo, la lista de salida puede tener elementos como estos: (hacerlo)

["C:\Python31\Lib\site-packages\pygame\docs\ref\mask.html",
 "C:\Python31\Lib\site-packages\pygame\docs\ref\midi.html",
 ...
 "C:\Python31\Lib\site-packages\pygame\examples\aliens.py",
 ...
 "C:\Python31\Lib\site-packages\pygame\examples\data\boom.wav",
 ... ]

11) Escribe un programa llamado ensuciar.py que cree un archivo vacío llamado basura.txt en cada subdirectorio de un árbol de directorios dada la raíz del directorio como un argumento (o el directorio actual como valor por defecto). Ahora escribe un programa llamado limpieza.py que elimine todos esos archivos. (hacerlo)

• Pista #1: Usa el programa del ejemplo de la última sección de este capítulo como base para estos dos programas recursivos. Ya que vas a destruir archivos en tu disco, mejor que lo hagas bien, o corres el riesgo de perder archivos que te importan. Así que un buen consejo es que inicialmente simules la eliminación de los archivos - por ejemplo sólo imprimiendo los caminos completos de cada archivo que se supone que eliminarías. Una vez que te hayas convencido de que tu lógica es correcta, y constates que no estarías borrando los archivos incorrectos, puedes reemplazar la sentencia print por la orden real de eliminación.
• Pista #2: Mira en el módulo os en busca de una función que elimine archivos.