Cap. 14 - Algoritmos de Listas

14.1) Desarrollo orientado a testeo (Test Driven Development, TDD)

En el capítulo 6, funciones fructíferas, presentamos la idea de desarrollo incremental, que consiste en ir agregando pequeños fragmentos de código para ir lentamente construyendo el todo, de forma de atajar los problemas a tiempo. Más adelante en ese mismo capítulo presentamos el concepto de testeo de unidades, y vimos código para nuestro entorno de testeo que nos permitiera formular, en código, una serie de testeos apropiados para las funciones que estuviéramos escribiendo.

El Desarrollo Orientado a Testeo (Test Driven Development, TDD) es una práctica de desarrollo de software que lleva estos principios un paso más allá. La idea clave es que los testeos automatizados deberían escribirse primero. Esta técnica se llama orientada a testeo porque - si debemos creer a los extremistas - el código que no es de testeo sólo debería escribirse cuando se tiene un testeo que ya está fallando y que es necesario superar.

Podemos aun retener nuestro modo de trabajo en pequeños pasos incrementales, pero ahora definiremos dichos pasos en términos de una secuencia de unidades de testeo cada vez más sofisticadas, que exigirán más a nuestro código en cada etapa.

Vamos a ver ahora algunos algoritmos estándar para procesar listas, pero a medida que avancemos en este capítulo trataremos de integrar a nuestro trabajo las exigencias del método TDD.

14.2) Algoritmo de búsqueda lineal

Nos gustaría saber en qué índice de una lista aparece por primera vez un ítem. Específicamente, retornaremos el índice del ítem si es encontrado, o retornaremos -1 si no aparece en la lista.

Comencemos con algunos tests: (L14_listas.py)

amigos = ["Juan", "Pedro", "Santiago", "Marta", "María", "Raquel", "José"]
test(busqueda_lineal(amigos, "Pedro") == 1)
test(busqueda_lineal(amigos, "Juan") == 0)
test(busqueda_lineal(amigos, "Raquel") == 5)
test(busqueda_lineal(amigos, "Daniel") == -1)

Motivados por el hecho de que nuestros tests ni siquiera corren, y mucho menos pasan, escribimos ahora la función: (L14_listas.py)

def busqueda_lineal(xs, aguja):
    """
        Buscar aguja en xs y devolver su índice en caso de encontrarla
        En caso contrario retornar -1
    """
    for (i, v) in enumerate(xs):
       if v == aguja:
           return i
    return -1

Hay algunas cuestiones puntuales para aprender aquí: ya vimos un algoritmo similar en la sección 8.10 cuando buscábamos un carácter en un string. Allí usamos un loop while, mientras que aquí usamos un loop for, acoplado con enumerate para extraer los pares (i, v) en cada iteración. Hay otras variantes - por ejemplo, pudimos haber utilizado range y haber hecho el loop recorrer todos los índices, o podríamos haber utilizado la convención de retornar None cuando el item no se encuentra en la lista. Pero la similitud esencial en todas estas variantes es que revisamos todos los items de la lista por turnos, del primero al último, utilizando el patrón de la recorrida eureka con corto-circuito que introdujimos antes (sección 8.10) - a saber, que retornamos de la función tan pronto como hayamos encontrado la aguja que estamos buscando.

La búsqueda que se realiza recorriendo todos los ítems desde el primero al último se llama búsqueda lineal. Cada vez que chequeamos si v == aguja lo llamamos una prueba. Nos gusta contar pruebas como una medida de cuán eficiente es nuestro algoritmo, y esto será una indicación bastante buena de cuánto tiempo requerirá la ejecución de nuestro algoritmo.

La búsqueda lineal se caracteriza por el hecho de que la cantidad de pruebas requeridas para encontrar cierta aguja depende directamente del largo de la lista. Si la lista es 10 veces más grande, es de esperar que necesitemos 10 veces más tiempo de búsqueda. Cabe observar también que si buscamos una aguja que no está en la lista, debermos ir hasta el final de la lista antes de poder retornar un valor negativo. Así que este caso necesita N pruebas, donde N es el caso de la lista. Sin embargo, si buscamos una aguja que existe en la lista, podríamos tener la suerte de que justo esté en la posición 0, o podríamos tener la mala suerte de que esté más adelante, siendo el peor de los casos cuando justo fuera el último ítem. En promedio, cuando la aguja está en la lista, deberemos ir hasta la mitad de la misma, o sea N/2 pruebas.

Decimos que esta búsqueda tiene rendimiento lineal (donde lineal hace referencia a una línea recta) porque, si fuéramos a medir el tiempo promedio de búsqueda para distintos tamaños de N, y luego hiciéramos un gráfico del tiempo de búsqueda en función de N, obtendríamos aproximadamente el gráfico de una línea recta.

Un análisis como el que venimos haciendo casi no tiene sentido para ciertas listas - la computadora es lo suficientemente rápida como para que no importe todo esto, si la lista tiene unos pocos elementos. Pero en general nos interesa la escalabilidad de nuestros algoritmos - cómo se comportan si les proponemos casos de tamaño más grande. ¿Sería esta búsqueda un modo razonable de proceder si tuviéramos millones o decenas de millones de items? (el tamaño del catálogo de libros de una biblioteca pública de tamaño normal). ¿Y qué pasa por conjuntos aun más grandes de datos, por ejemplo, cómo hace Google para buscar tan rápido entre miles de billones, o incluso billones, de páginas?

14.3) Un problema más realista

A medida que los niños aprender a leer, se espera que su vocabulario vaya creciendo. Por lo tanto se espera que un adolescente de 14 años maneje un vocabulario mayor que un niño de 8. Cuando se prescribe la lectura de libros para un cierto grado, una cuestión importante es "qué palabras de este libro no están en el vocabulario que es de esperar en un lector de esta edad?"

Supongamos que podemos leer un vocabulario de palabras en nuestro programa, y leer el texto del libro, y dividirlo en palabras. Escribamos algunos tests para lo que necesitaremos hacer más adelante. Los datos de testeo pueden ser pequeños, incluso si después vamos a usar nuestro programa con entradas más grandes: (L14_listas.py)

vocabulario = ["manzana", "niño", "perro", "abajo",
                          "cayó", "niña", "pasto", "el", "la", "árbol"]
palabras_libro = "la manzana cayó desde el árbol hasta el pasto".split()
test(encontrar_palabras_desconocidas(vocabulario, palabras_libro) == ["desde", "hasta"])
test(encontrar_palabras_desconocidas([], palabras_libro) == palabras_libro)
test(encontrar_palabras_desconocidas(vocabulario, ["el", "niño", "cayó"]) == [])

• Observación: los tests anteriores, y la implementación que sigue, asumen que si una palabra del libro que no está en el vocabulario aparece más de una vez, será retornada más de una vez por la función.

Observar que fuimos un poco vagos, y utlizamos el método split para crear nuestra lista de palabras.

• Es más fácil que escribir la lista, y muy conveniente si se quiere introducir una frase en un programa convertida en una lista de palabras.

Ahora necesitamos implementar la función para la cual ya escribimos los tests, y haremos uso de la búsqueda lineal. La estrategia básica es recorrer cada una de las palabras del libro, ver si está en el vocabulario, y si no está en el vocabulario, guardarla en una nueva lista resultante que retornamos desde la función. (L14_listas.py)

def encontrar_palabras_desconocidas(vocab, pals):
    """ Retorna una lista de palabras que son todas las que están en pals pero no aparecen en vocab """
    result = []
    for pal in pals:
        if (busqueda_lineal(vocab, pal) < 0):
            result.append(pal)
    return result

Constatamos con felicidad que han pasado todos los tests.

Pero ocupémenos ahora de la escalabilidad. Tenemos un vocabulario más realista en el archivo que bajamos al principio de este capítulo, así que leamos ese archivo para dividirlo en una lista de palabras. Por conveniencia, crearemos una función que lo haga por nosotros, y la testearemos con el archivo que tenemos disponible: (L14_listas.py)

def leer_palabras_de_archivo(archivo):
    """ Lee palabras del archivo, retorna una lista de palabras. """
    f = open(filename, "r")
    f_contenido = f.read()
    f.close()
    pals = f_contenido.split()
    return pals

gran_vocabulario = leer_palabras_de_archivo("vocab.txt")
print("Hay {0} palabras en el vocab, comenzando con \n {1} "
              .format(len(gran_vocabulario), gran_vocabulario[:6]))

• Observación: para lo que hace el vocabulario, hubiera sido razonable no incluir en el valor retornado palabras repetidas - esta implementación no tiene en cuenta ese detalle y retorna repetidas.

Python responde así:

Hay 19455 palabras en el vocab, comenzando con 
 ['a', 'aback', 'abacus', 'abandon', 'abandoned', 'abandonment'] 

Así que ahora tenemos un vocabulario de tamaño más respetable. Ahora vamos a leer un libro, y una vez más utilizaremos el archivo que bajamos al comienzo de este capítulo. Leer un libro es similar a leer palabras de un archivo, pero aplicaremos un par de trucos extra. Los libros están llenos de puntuación y mezcla de mayúsculas y minúsculas. Necesitamos limpiar el contenido del libro, para lo cual eliminaremos la puntuación, y convertiremos todo a minúsculas (ya que nuestro vocabulario está en minúsculas). Así que tenemos que mejorar nuestra función que convierte texto en palabras: (L14_listas.py)

test(texto_a_palabras("My name is Earl!") == ["my", "name", "is", "earl"])
test(texto_a_palabras('"Well, I never!", said Alice.') ==
                             ["well", "i", "never", "said", "alice"])

Hay un método muy poderoso disponible para strings, llamado translate. La idea es que uno primero define ciertas sustituciones deseables (para cada carácter, podemos definir un carácter correspondiente de reemplazo). El método translate aplicará estos reemplazos a lo largo de todo el string. Aprovechémoslo para implementar nuestra función: (L14_listas.py)

def texto_a_palabras(texto):
    """ retorna una lista de palabras con la puntuación eliminada,
        y todo en minúsculas.
    """

    mis_sustituciones = texto.maketrans(
      # Si encontrás cualquiera de éstas
      "ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789!\"#$%&()*+,-./:;<=>?@[]^_`{|}~'\\",
      # Reemplazarla con éstas
      "abcdefghijklmnopqrstuvwxyz                                          ")

    # Trasladar el texto ahora.
    texto_limpio = texto.translate(mis_sustituciones)
    pals = texto_limpio.split()
    return pals

La traducción que acabamos de definir (mediante el método translation) convierte todas las mayúsculas en minúsculas, y todos los signos de puntuación en espacios.

• Cabe observar que si quisiéramos utilizarla en idioma español, deberíamos agregar traducciones para caracteres como Ñ, Á, É, etc.

Luego la función split se ocupa de eliminar todos los espacios, al desarmar el texto y convertirlo en una lista de palabras. Y nuestros tests pasan.

Ahora podemos leer en nuestro libro:

def obtener_palabras_de_libro(archivo_libro):
    """ Lee un libro de archivo_libro y retorna una lista con sus palabras. """
    f = open(archivo_libro, "r")
    contenido = f.read()
    f.close()
    pals = texto_a_palabras(contenido)
    return pals

palabras_libro = obtener_palabras_de_libro("alice_in_wonderland.txt")
print("Hay {0} palabras en el libro, y las primeras 100 son\n{1}".
           format(len(palabras_libro), palabras_libro[:100]))

Python imprime lo siguiente (todo en una línea - pero lo modificamos para que se lea bien en la caja de texto)

Hay 27336 palabras en el libro, y las primeras 100 son
['alice', 's', 'adventures', 'in', 'wonderland', 'lewis', 'carroll', 'chapter', 'i', 'down', 'the', 'rabbit', 'hole', 
'alice', 'was', 'beginning', 'to', 'get', 'very', 'tired', 'of', 'sitting', 'by', 'her', 'sister', 'on', 'the', 'bank', 'and', 'of', 
'having', 'nothing', 'to', 'do', 'once', 'or', 'twice', 'she', 'had', 'peeped', 'into', 'the', 'book', 'her', 'sister', 'was', 
'reading', 'but', 'it', 'had', 'no', 'pictures', 'or', 'conversations', 'in', 'it', 'and', 'what', 'is', 'the', 'use', 'of', 'a', '
book', 'thought', 'alice', 'without', 'pictures', 'or', 'conversation', 'so', 'she', 'was', 'considering', 'in', 'her', 
'own', 'mind', 'as', 'well', 'as', 'she', 'could', 'for', 'the', 'hot', 'day', 'made', 'her', 'feel', 'very', 'sleepy', 'and', 
'stupid', 'whether', 'the', 'pleasure', 'of', 'making', 'a']

Con esto ya tenemos todas las partes del programa prontas. Veamos ahora qué palabras del libro no están en el vocabulario:

>>> palabras_faltantes = encontrar_palabras_desconocidas(gran_vocabulario, palabras_libro)

Hay que esperar una buena cantidad de tiempo, más o menos un minuto, antes de que Python logre terminar de ejecutar el algoritmo e imprima una lista de 3396 palabras del libro que no están en el vocabulario. Es decir que tenemos un problema: este método no es realmente escalable. Si nuestro vocabulario fuera 20 veces mayor (es frecuente encontrar diccionarios escolares con 300.000 palabras, por ejemplo), y tuviéramos que analizar un libro más largo, tardaremos demasiado tiempo. Así que hagamos algunas mediciones de tiempo mientras vamos pensando cómo podríamos mejorar este desempeño en la próxima sección.

import time

t0 = time.time()
palabras_faltantes = encontrar_palabras_desconocidas(gran_vocabulario, palabras_libro)
t1 = time.time()
print("Hay {0} palabras desconocidas.".format(len(palabras_faltantes)))
print("Esto llevó {0:.4f} segundos.".format(t1-t0))

Hay 3396 palabras desconocidas.

Esto llevó 51.3028 segundos.

14.4) Búsqueda binaria

Si te detienes a pensar en lo que acabamos de hacer, no es como lo haríamos en la vida real. Si te dieran un vocabulario y te preguntaran si alguna palabra está presente, probablemente comenzarías por la mitad. Puedes hacerlo porque el vocabulario está ordenado - entonces probás con alguna palabra en el medio, y de inmediato te das cuenta de que tenés que buscar antes (o después) de la que probaste. Aplicando este principio repetidamente nos lleva a un algoritmo mucho mejor para buscar en una lista items que ya están ordenados (observar que si los items del vocabulario no están ordenados, no habrá más remedio que recorrerlos a todos - pero si los tenemos ordenados, podemos mejorar nuestra técnica de búsqueda).

Comencemos con algunos tests. Recordemos que tenemos que ordenar la lista:

xs = [2,3,5,7,11,13,17,23,29,31,37,43,47,53]
test(busqueda_binaria(xs, 20) == -1)
test(busqueda_binaria(xs, 99) == -1)
test(busqueda_binaria(xs, 1) == -1)
for (i, v) in enumerate(xs):
    test(busqueda_binaria(xs, v) == i)

Incluso nuestros casos de testeo son interesantes esta vez: observar que comenzamos con items que no están en la lista y vamos por condiciones de borde - en el medio de la lista, menor que el primer elemento de la lista, mayor que el último elemento de la lista. Luego utilizamos un loop para tratar a cada elemento de la lista como una aguja, y confirmar que nuestra búsqueda binaria retorne el índice correspondiente a dicho ítem en la lista.

Es útil pensar que tenemos una región de interés (ROI, region of interest) en la lista en que estamos buscando. Esa ROI será la porción de la lista en que es posible que sea encontrada nuestra aguja. Nuestro algoritmo comenzará con una ROI igual a todos los elementos de la lista. Tras una primera prueba en el medio de la ROI, hay 3 posibles resultados: o encontramos la aguja, o aprendemos que podemos descartar la mitad superior de la ROI, o aprendemos que podemos descartar la mitad inferior de la ROI. Y hacemos esto repetidamente, hasta que encontramos nuestra aguja, o hasta que terminemos sin elementos en nuestra ROI.

Todo esto lo podemos implementar así:

def busqueda_binaria(xs, aguja):
    """ Encontrar y retornar el índice de la aguja en la secuencia xs
            (o retornar -1 si no se encuentra) """
    borde_inferior = 0
    borde_superior = len(xs)
    while True:
        if borde_inferior == borde_superior:   # Si la región de interés (ROI) quedó vacía
           return -1

        # La próxima prueba debería ser en el medio de la ROI
        indice_medio = (borde_inferior + borde_superior) // 2

        # Obtener el item en esa posición
        item_del_medio = xs[indice_medio]

        # print("ROI[{0}:{1}](tamaño={2}), probado='{3}', buscado='{4}'"
        #       .format(borde_inferior, borde_superior, borde_superior-borde_inferior, item_del_medio, aguja))

        # Cómo se compara el item probado con el item buscado?
        if item_del_medio == aguja:
            return indice_medio      # Lo encontramos!
        if item_del_medio < aguja:
            borde_inferior = indice_medio + 1    # Usar la mitad superior de la ROI en el siguiente paso
        else:
            borde_superior = indice_medio        # Usar la mitad inferior de la ROI en el siguiente paso

La región de interés (ROI) es representada por 2 variables, un límite inferior borde_inferior y un límite superior borde_superior. Es importante ser precisos con los valores que tienen estos índices. Haremos que borde_inferior corresponda al índice del primer item de la ROI, y que borde_superior tenga el índice del primer item más allá del último ítem de la ROI. Es decir que nuestra semántica es similar a la del método slice de Python: la región de interés es exactamente el trozo (slice) xs[borde_inferior : borde_superior].

• Observación: lo anterior es una observación conceptual. El algoritmo de hecho nunca utiliza el método slice para recortar listas!

Con este código, la función busqueda_binaria pasa los tests. Muy bien. Ahora si sustituimos el viejo llamado a busqueda_lineal por un llamado a busqueda_binaria en la función encontrar_palabras_desconocidas, ¿podremos mejorar la performance? Probemos, corriendo de nuevo el test que buscaba palabras faltantes:

t0 = time.time()
palabras_faltantes = encontrar_palabras_desconocidas(gran_vocabulario, palabras_libro)
t1 = time.time()
print("Hay {0} palabras desconocidas.".format(len(palabras_faltantes)))
print("Esto llevó {0:.4f} segundos.".format(t1-t0))

¡Qué diferencia espectacular! ¡Casi 200 veces más rápido!

Hay 3396 palabras desconocidas.
Esto llevó 0.3133 segundos.

¿Por qué esta búsqueda binaria es tanto más rápida que la lineal? Si quitamos los comentarios de las líneas print de la función busqueda_binaria, podremos seguirle las huellas a las pruebas hechas durante una búsqueda. Hagámoslo una vez:

>>> busqueda_binaria(gran_vocabulario, "magic")
ROI[0:19455](tamaño=19455), probado='knowing', buscado='magic'
ROI[9728:19455](tamaño=9727), probado='resurgence', buscado='magic'
ROI[9728:14591](tamaño=4863), probado='overslept', buscado='magic'
ROI[9728:12159](tamaño=2431), probado='misreading', buscado='magic'
ROI[9728:10943](tamaño=1215), probado='magnet', buscado='magic'
ROI[9728:10335](tamaño=607), probado='lightning', buscado='magic'
ROI[10032:10335](tamaño=303), probado='longitudinal', buscado='magic'
ROI[10184:10335](tamaño=151), probado='lumber', buscado='magic'
ROI[10260:10335](tamaño=75), probado='lyrical', buscado='magic'
ROI[10298:10335](tamaño=37), probado='made', buscado='magic'
ROI[10317:10335](tamaño=18), probado='magic', buscado='magic'
10326

Vemos aquí que encontrar la palabra buscada "magic" sólo llevó 14 pasos hasta descubrirse que le correspondía el índice 10326. Lo importante aquí es que cada prueba reduce a la mitad (a menos de un truncamiento) la siguiente región de interés. Por el contrario, la búsqueda binaria hubiera necesitado 10327 pruebas para encontrar la misma palabra.

La palabra binario se refiere al número dos. La búsqueda binaria toma su nombre del hecho de que cada prueba divide la lista en dos partes y descarta una mitad de la región de interés.

La belleza del algoritmo es que podríamos duplicar el tamaño del vocabulario, y sólo necesitaríamos una prueba extra! Y si duplicamos otra vez, sólo una prueba más! De modo que a medida que crece el vocabulario, la performance del algoritmo se vuelve más y más impresionante.

¿Podemos expresar esto con una fórmula? Si nuestra lista tiene tamaño N, cuál es el máximo número k de pruebas que vamos a necesitar? Las matemáticas del problema se simplifican si hacemos la pregunta al revés: cuán grande puede ser una lista de tamaño N, sabiendo que no se nos permite hacer más de k pruebas?

• Si se nos permite 1 prueba, sólo podemos buscar una lista de tamaño 1.
• Con dos pruebas podríamos manejar una lista de tamaño 3 (probamos el ítem del medio con la primera prueba, y luego testeamos el de la izquierda o el de la derecha con la segunda prueba).
• Con 3 pruebas, podríamos testear una lista de tamaño 7: el ítem del medio, y dos sublistas de tamaño 3.
• Con 4 pruebas, podemos buscar 15 items (el del medio y dos listas de 7)
• Con 5 pruebas, podemos buscar 31 (el del medio y dos listas de 15)

Así que la relación general viene dada por la fórmula:

• donde k es el número de pruebas que se nos permite hacer
• y N es el máximo tamaño de la lista que puede ser buscada con esas pruebas

La función es exponencial en k (dado que k está en la parte del exponente). Si quisiéramos invertir la ecuación para despejar k y ponerlo en función de N, debemos mover la constante 1 para el otro lado, y tomar un logaritmo (base 2) de cada lado (porque la función logaritmo es la inversa de la exponencial, para una base dada). Así que la fórmula para k en función de N es ahora:

Los corchetes solo cuadrados en la parte superior se llaman corchetes techo: significan que hay que redondear el número al próximo entero (el inmediatamente mayor disponible).

Intentémoslo en una calculadora, o en Python, que es la madre de todas las calculadoras: supongamos que tenemos 1000 elementos para buscar, entonces, ¿cuál sería el máximo número de pruebas que necesitaría? (no olvidemos especialmente el molesto "+ 1" de la fórmula). Hacemos esto:

>>> from math import log
>>> log(1000 + 1, 2)
9.967226258835993

Esto nos dice que necesitaremos 9.96 pruebas como máximo para buscar 1000 items. No debemos olvidar tomar el techo, o sea el entero inmediatamente superior a 9.96 en este ejemplo. La función ceil del módulo math hace exactamente eso. Así que podemos mejorar el código anterior para hacerlo coincidir completamente con nuestra fórmula matemática, así:

>>> from math import log, ceil
>>> ceil(log(1000 + 1, 2))
10
>>> ceil(log(1000000 + 1, 2))
20
>>> ceil(log(1000000000 + 1, 2))
30

Esto nos dice que buscar en una lista de 1000 items requerirá 10 pruebas. Buscar una de 1 millón de items requerirá 20 pruebas. Y buscar una de 1000 millones de items requerirá 30 pruebas. Podemos ya adivinar que 1 billón de items requerirán 40 pruebas, y 1 trillón 60 pruebas.

Muy pocas veces en tu vida de programador te vas a encontrar con un algoritmo que lidie tan exitosamente con entradas grandes como lo hace busqueda_binaria!

14.5) Eliminando duplicados adyacentes de una lista

Muchas veces queremos obtener elementos únicos de una lista, es decir, producir una nueva lista en que no hay elementos repetidos. Consideremos el caso en que buscábamos palabras en Alicia en el País de las Maravillas que no estuvieran en nuestro vocabulario. Obtuvimos el reporte de que había 3396 palabras así, pero la lista tenía duplicados. De hecho, la palabra "alice" ocurre 398 veces en el libro, y no está en nuestro vocabulario! ¿Cómo deberíamos eliminar estos duplicados?

Un buen método es ordenar la lista, y luego eliminar todos los duplicados adyacentes. Comencemos por eliminar duplicados adyacentes de una lista ya ordenada:

test(eliminar_duplicados_adyacentes([1,2,3,3,3,3,5,6,9,9]) == [1,2,3,5,6,9])
test(eliminar_duplicados_adyacentes([]) == [])
test(eliminar_duplicados_adyacentes(["a", "big", "big", "bite", "dog"]) ==
                                   ["a", "big", "bite", "dog"])

El algoritmo es fácil y eficiente. Simplemente debemos recordar el último ítem que fue insertado en el resultado, y evitar reinsertarlo en caso de aparecer otra vez:

def eliminar_duplicados_adyacentes(xs):
    """ Retorna una nueva lista en la que han sido eliminados
        todos los duplicados adyacentes de xs.
    """
    resultado = []
    elemento_mas_reciente = None
    for e in xs:
        if e != elemento_mas_reciente:
            resultado.append(e)
            elemento_mas_reciente = e

    return resultado

La cantidad de trabajo realizado en este algoritmo es lineal - cada item de xs hace que el loop se ejecute una sola vez, y no hay loops anidados. Así que si duplicamos el número de elementos de xs nuestra función requerirá el doble del tiempo para ejecutarse: la relación entre el tamaño de la lista y el tiempo para ejecutar la función se graficaría como una línea recta.

Volvamos ahora a nuestro análisis de Alicia en el País de las Maravillas. Antes de chequear las palabras en el libro con nuestro vocabulario, ordenaremos las palabras y eliminaremos duplicados. Así que nuestro nuevo código se ve así:

todas_las_palabras = obtener_palabras_de_libro("alice_in_wonderland.txt")
todas_las_palabras.sort()
palabras_libro = eliminar_duplicados_adyacentes(todas_las_palabras)
print("Hay {0} palabras en el libro. Sólo {1} son únicas.".
                      format(len(todas_las_palabras), len(palabras_libro)))
print("Las primeras 100 palabras (por orden alfabético) son\n{0}".
           format(palabras_libro[:100]))

Casi mágicamente, obtenemos el siguiente output:

Hay 27336 palabras en el libro. Sólo 2569 son únicas.
Las primeras 100 palabras (por orden alfabético) son
['a', 'abide', 'able', 'about', 'above', 'absence', 'absurd', 'acceptance', 'accident', 'accidentally', 'account', 'accounting', 'accounts', 'accusation', 'accustomed', 'ache', 'across', 'act', 'actually', 'ada', 'added', 'adding', 'addressed', 'addressing', 'adjourn', 'adoption', 'advance', 'advantage', 'adventures', 'advice', 'advisable', 'advise', 'affair', 'affectionately', 'afford', 'afore', 'afraid', 'after', 'afterwards', 'again', 'against', 'age', 'ago', 'agony', 'agree', 'ah', 'ahem', 'air', 'airs', 'alarm', 'alarmed', 'alas', 'alice', 'alive', 'all', 'allow', 'almost', 'alone', 'along', 'aloud', 'already', 'also', 'altered', 'alternately', 'altogether', 'always', 'am', 'ambition', 'among', 'an', 'ancient', 'and', 'anger', 'angrily', 'angry', 'animal', 'animals', 'ann', 'annoy', 'annoyed', 'another', 'answer', 'answered', 'answers', 'antipathies', 'anxious', 'anxiously', 'any', 'anything', 'anywhere', 'appealed', 'appear', 'appearance', 'appeared', 'appearing', 'applause', 'apple', 'apples', 'arch', 'archbishop']

Lewis Carroll fue capaz de escribir un clásico de la literatura usando apenas 2569 palabras!

14.6) Fusión (merging) de listas ordenadas

Supongamos que tenemos dos listas ordenadas. Buscamos un algoritmo que nos permita combinar a ambas para formar una única lista ordenada.

Una forma simple pero muy eficiente sería la siguiente: juntar primero las dos listas poniendo una al final de la otra, y luego ordenar el resultado:

nueva_lista = (xs + ys)
nueva_lista.sort()

Este método no aprovecha el hecho de que las dos listas ya están ordenadas, y va a tener una pobre escalabilidad y mala performance para listas muy grandes.

Definamos primero algunos tests:

xs = [1,3,5,7,9,11,13,15,17,19]
ys = [4,8,12,16,20,24]
zs = xs+ys
zs.sort()
test(combinar_listas_ordenadas(xs, []) == xs)
test(combinar_listas_ordenadas([], ys) == ys)
test(combinar_listas_ordenadas([], []) == [])
test(combinar_listas_ordenadas(xs, ys) == zs)
test(combinar_listas_ordenadas([1,2,3], [3,4,5]) == [1,2,3,3,4,5])
test(combinar_listas_ordenadas(["a", "big", "cat"], ["big", "bite", "dog"]) ==
               ["a", "big", "big", "bite", "cat", "dog"])

Aquí está nuestro algoritmo combinar_listas_ordenadas:

def combinar_listas_ordenadas(xs, ys):
    """ combina las listas ordenadas xs e ys. Retorna una lista ordenada única """
    resultado = []
    xi = 0
    yi = 0

    while True:
        if xi >= len(xs):              # Si terminamos la lista xs,
            resultado.extend(ys[yi:])  # Agregar los items que quedan de ys
            return resultado           # Y terminamos.

        if yi >= len(ys):              # Lo mismo, pero invirtiendo roles
            resultado.extend(xs[xi:])
            return resultado

        # Ambas listas aun tienen items, copiar el más pequeño a resultado.
        if xs[xi] <= ys[yi]:
            resultado.append(xs[xi])
            xi += 1
        else:
            resultado.append(ys[yi])
            yi += 1

El algoritmo funciona de la siguiente manera: creamos una lista de resultados, y mantenemos dos índices, cada uno a cada lista (líneas 3-5). En cada iteración del loop, el ítem que sea más pequeño es copiado a la lista de resultados, y el índice de la lista correspondiente avanza un lugar. Tan pronto como alguno de los dos índices alcance el final de su lista respectiva, copiamos los items restantes de la otra en la lista de resultados, la cual luego retornamos.

14.7) Alicia en el País de las Maravillas, otra vez!

Subyacente al algoritmo que combina dos listas ordenadas hay un patrón importante de computación que es ampliamente reutilizable. El patrón en esencia es "Recorre las listas procesando siempre al menor de los ítems que quedan de cada una, con estos casos a considerar"

• Qué debemos hacer cuando alguna de las listas ya no tenga elementos?
• Qué debemos hacer si los menores elementos de ambas listas coinciden?
• Qué debemos hacer si el menor elemento de la primera lista es menor que el menor de la segunda lista?
• Qué debemos hacer en el caso contrario?

Supongamos que tenemos dos listas ordenadas. Ejercita tus habilidades algorítmicas adaptando este patrón algorítmico para cada uno de estos casos: (implementarlos)

• Retornar sólo los elementos que están presentes en ambas listas.
• Retornar sólo los elementos que aparecen en la primera lista, pero no en la segunda.
• Retornar sólo los elementos que aparecen en la segunda lista, pero no en la primera.
• Retornar sólo elementos que están presentes o bien en la primera o bien en la segunda lista, pero no en ambas.
• Retornar elementos de la primera lista que no son eliminados por un elemento correspondiente en la segunda lista.
  
  • En este caso, un item en la segunda lista hace "knock out" a sólo un elemento de la primera lista que sea igual a él (no a todos los que sean iguales a él)
  • Esta operación a veces se llama bagdiff
  • Por ejemplo: bagdiff([5,7,11,11,11,12,13], [7,8,11]) retornaría [5, 11, 11, 12, 13]

En la sección previa ordenamos las palabras del libro, y eliminamos duplicados. Nuestro vocabulario también está ordenado. Así que el tercer caso planteado arriba - encontrar todos los items que aparecen en la segunda lista, pero no en la primera - sería otra forma de implementar encontrar_palabras_desconocidas. En vez de buscar por cada palabra en el diccionario (sea por búsqueda lineal o por búsqueda binaria), ¿por qué no usar una variante del algoritmo de combinación para retornar las palabras que ocurren en el libro, pero no en el vocabulario?

def combinar_listas_ordenadas(xs, ys):
    """ combina las listas ordenadas xs e ys. Retorna una lista ordenada única """
    resultado = []
    xi = 0
    yi = 0

    while True:
        if xi >= len(xs):              # Si terminamos la lista xs,
            resultado.extend(ys[yi:])  # Agregar los items que quedan de ys
            return resultado           # Y terminamos.

        if yi >= len(ys):              # Lo mismo, pero invirtiendo roles
            resultado.extend(xs[xi:])
            return resultado

        # Ambas listas aun tienen items, copiar el más pequeño a resultado.
        if xs[xi] <= ys[yi]:
            resultado.append(xs[xi])
            xi += 1
        else:
            resultado.append(ys[yi])
            yi += 1

Ahora ponemos a funcionar todo junto:

gran_vocabulario = leer_palabras_de_archivo("vocab.txt")
todas_las_palabras = obtener_palabras_de_libro("alice_in_wonderland.txt")
t0 = time.time()
todas_las_palabras.sort()
palabras_libro = eliminar_duplicados_adyacentes(todas_las_palabras)
palabras_faltantes = encontrar_palabras_desconocidas(gran_vocabulario, palabras_libro)
t1 = time.time()
print("Hay {0} palabras desconocidas.".format(len(palabras_faltantes)))
print("Esto llevó {0:.4f} segundos.".format(t1-t0))

Y la performance es aun más impresionante que antes:

Hay 827 palabras desconocidas.
Esto llevó 0.0470 segundos.

Repasemos lo que hemos hecho. Comenzamos con una búsqueda lineal palabra por palabra en el vocabulario que tardó unos 50 segundos en ejecutarse. Luego implementamos una búsqueda binaria bastante más ingeniosa, y el tiempo se redujo a unos 0.30 segundos, casi 200 veces más rápido. Pero entonces hicimos algo todavía mejor: ordenamos las palabras del libro, eliminamos duplicados, y aplicamos un patrón de combinación (merging pattern) para encontrar palabras del libro que no estuvieran en el vocabulario. Esto fue más de 5 veces más rápido incluso que la recorrida con búsqueda binaria. Este algoritmo que alcanzamos al final del proceso es unas 1000 veces más rápido que el de nuestro primer intento!

Eso es lo que se llama un buen día en la oficina!

14.8) El problema de las 8 reinas, parte 1

Como lo define Wikipedia, "El problema de las ocho reinas es un pasatiempo que consiste en poner ocho reinas en el tablero de ajedrez sin que se amenacen. Fue propuesto por el ajedrecista alemán Max Bezzel en 1848."

• Por lo tanto, cualquier solución del problema requiere que no haya dos reinas en la misma columna, fila o diagonal.

Una solución posible se ve en la siguiente imagen:

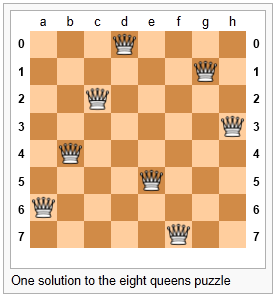
Es recomendable que lo intentes a mano, y encuentres al menos un par de soluciones más.

Nos gustaría escribir un programa que encuentre soluciones a este puzzle. De hecho, el puzzle se puede generalizar a ubicar N reinas en un tablero de N*N dimensiones, así que pensaremos el caso general y no sólo el de 8*8. Tal vez podamos encontrar soluciones al problema de ubicar 12 reinas en un tablero de 12*12, o 20 reinas en un tablero de 20*20.

¿Cómo encarar un problema tan complejo como éste? Un buen comienzo sería pensar en nuestras estructuras de datos - cómo vamos a representar exactamente el tablero de ajedrez y sus reinas en nuestro programa. Una vez que tengamos cierta idea de cómo se va a ver nuestro tablero en memoria, podremos comenzar a razonar en cuanto a qué funciones y qué lógica serán necesarias para resolver nuestro problema, es decir, cómo ponemos una reina más en el tablero y cómo verificamos si esto general problemas con las que ya tenemos en el puestas.

Los pasos para encontrar una buena representación, y luego un buen algoritmo para operar en los datos, no siempre se pueden hacer por separado. A medida que pienses en las operaciones que serán necesarias, puede que decidas modificar o reorganizar la forma en que guardas los datos para de alguna forma hacer más fácil la implementación de las operaciones requeridas.

Esta relación entre algoritmos y datos fue elegantemente expresada en el título del libro Algoritmos + Estructuras de Datos = Programas, escrito por uno de los pioneros de la ciencia de la computación, Niklaus Wirth, el inventor del lenguaje de programación Pascal.

Comencemos por hacer una lista de ideas en cuanto a cómo podríamos representar el tablero y las reinas en memoria:

• Una matriz bidimensional (una lista de 8 listas, cada una conteniendo 8 cuadros) es una posibilidad. En cada cuadro del tablero nos interesa saber si contiene una reina o no - sólo hay dos estados posibles para cada cuadro - así que tal vez cada elemento de las listas podría ser True o False, o más simplemente, 0 o 1.

• Nuestro estado para la solución anterior podría entonces tener la siguiente representación de datos:

bd1 = [[0,0,0,1,0,0,0,0],
       [0,0,0,0,0,0,1,0],
       [0,0,1,0,0,0,0,0],
       [0,0,0,0,0,0,0,1],
       [0,1,0,0,0,0,0,0],
       [0,0,0,0,1,0,0,0],
       [1,0,0,0,0,0,0,0],
       [0,0,0,0,0,1,0,0]]

• También deberías ser capaz de ver cómo se representaría el tablero vacío, y comenzar a imaginar qué clase de operaciones o modificaciones deberías hacer a los datos para ubicar a otra reina en algún punto del tablero.

• Otra idea podría ser mantener una lista de coordenadas indicando dónde se ubican las reinas. Podríamos entonces representar la solución de la ilustración anterior de esta forma:

bd2 = [ "a6", "b4", "c2", "d0", "e5", "f7", "g1", "h3" ]

• Una variante más manejable para un programador sería mantener una lista de tuplas, con coordenadas enteras para cada eje. Y como ya pensamos como programadores, comenzaremos a contar desde 0 en vez de 1. Ahora nuestra representación sería:

bd3 = [(0,6), (1,4), (2,2), (3,0), (4,5), (5,7), (6,1), (7,3)]

• Si miramos con atención la representación anterior, veremos que el primer elemento de cada tupla corresponde al índice de los pares en cada lista. Así que podemos descartarlo, y llegar a esta representación realmente compacta de la solución de la figura anterior:

bd4 = [6, 4, 2, 0, 5, 7, 1, 3]

Usaremos esta última representación. Veamos ahora a dónde nos lleva.

Tratemos ahora de avanzar en la resolución del problema. ¿Es una coincidencia que no haya números repetidos en la solución? La solución [6,4,2,0,5,7,1,3] contiene todos los números del 0 al 7, sin duplicar a ninguno. ¿Podría existir una solución con números duplicados?

Basta pensarlo un momento para comprender que no pueden haber números duplicados en una solución: los números representan la fila en que está ubicada la reina, y como no se nos permite tener dos reinas en la misma fila, ninguna solución podrá tener números duplicados en ella.

test(not comparten_diagonal(5,2,2,0))
test(comparten_diagonal(5,2,3,0))
test(comparten_diagonal(5,2,4,3))
test(comparten_diagonal(5,2,4,1))

def comparten_diagonal(x0, y0, x1, y1):
    """ Comparte (x0, y0) alguna diagonal con (x1, y1)? """
    dy = abs(y1 - y0)        # Calcular la distancia absoluta en y
    dx = abs(x1 - x0)        # Calcular la distancia absoluta en x
    return dx == dy          # Están en la misma diagonal si dx == dy

# Soluciones del problema, que no deberían tener ningún conflicto
test(not columna_tiene_conflictos([6,4,2,0,5], 4))
test(not columna_tiene_conflictos([6,4,2,0,5,7,1,3], 7))

# Más casos de testeo que en su mayoría deberían tener conflictos
test(columna_tiene_conflictos([0,1], 1))
test(columna_tiene_conflictos([5,6], 1))
test(columna_tiene_conflictos([6,5], 1))
test(columna_tiene_conflictos([0,6,4,3], 3))
test(columna_tiene_conflictos([5,0,7], 2))
test(not columna_tiene_conflictos([2,0,1,3], 1))
test(columna_tiene_conflictos([2,0,1,3], 2))

def columna_tiene_conflictos(ys, c):
    """ Retorna True si la reina en la columna c tiene conflictos
         con cualquiera de las reinas que están a su izquierda
    """
    for i in range(c):     # Mirar a todas las columnas a la izquierda de c
          if comparten_diagonal(i, ys[i], c, ys[c]):
              return True

    return False           # No hay conflicots - la columna c es apta para poner una reina.

test(not tiene_conflictos([6,4,2,0,5,7,1,3]))  # La solución dada más arriba
test(tiene_conflictos([4,6,2,0,5,7,1,3]))      # Si intercambiamos las filas 1 y 2, ya no funciona
test(tiene_conflictos([0,1,2,3]))              # Caso con el pequeño tablero 4x4
test(not tiene_conflictos([2,0,3,1]))              # Solución para el caso 4x4

def tiene_conflictos(tablero):
    """ Determina si tenemos reinas con conflictos de diagonales.
        Asumimos que tablero es una permutación de números de columnas
        (por lo cual no es necesario chequear explícitamente conflictos de filas o columnas).
    """
    for col in range(1, len(tablero)):
        if columna_tiene_conflictos(tablero, col):
            return True
    return False

14.9) El problema de las 8 reinas, parte 2

Esta es la parte fácil y divertida. Podríamos tratar de encontrar todas las permutaciones [0, 1, 2, 3, 4, 5, 6, 7] - lo cual sería de por sí un algoritmo interesante, y la forma de fuerza bruta de resolver el problema: probamos todas las configuraciones, y nos vamos fijando cuáles son soluciones.

Por supuesto sabemos que hay N! permutaciones de N cosas, así que nos podemos hacer rápidamente una idea de cuán largo sería encontrar todas las soluciones utilizando el método fuerza bruta. No sería demasiado largo para el problema de 8 reinas: 8! es tan sólo 40320. Esto es mucho mejor que comenzar con 64 lugares vacíos para ubicar 8 reinas. Si sacas la cuenta de cuántas formas podrías elegir 8 cuadros de los 64 para tus reinas, la fórmula (combinaciones de 8 tomadas de 64) da como resultado un impresionante 4.426.165.368, obtenido a partir de la fórmula: 64! / (8!56!).

Así que nuestra primera observación clave, aquella de que nos alcanzaba con sólo considerar permutaciones (de filas en columnas) redujo lo que llamamos el espacio del problema de unos 4.400 millones a tan sólo 40320!

Sin embargo, ni siquiera es necesario que revisemos esos 40320 casos. Cuando introdujimos el módulo de números aleatorios, aprendimos que tiene un método shuffle que permuta aleatoriamente una lista de items. Así que vamos a escribir un programa "aleatorio" para encontrar soluciones al problema de las 8 reinas. Comenzaremos con la permutación [0, 1, 2, 3, 4, 5, 6, 7] y repetidamente mezclaremos la lista (mediante el método shuffle), y testearemos cada caso a ver si es una solución. A medida que avancemos iremos contando cuántos intentos tuvimos que hacer hasta encontrar cada solución, y encontraremos 10 soluciones (puede que alguna de las 10 esté repetida, porque shuffle es aleatorio!).

def main():
    import random
    rng = random.Random()   # Instanciar al generador

    tablero = list(range(8))     # Generate la permutación inicial
    encontrados = 0
    intentos = 0
    while encontrados < 10:
       rng.shuffle(tablero)
       intentos += 1
       if not tiene_conflictos(tablero):
           print("Encontré la solución {0} en {1} intentos.".format(tablero, intentos))
           intentos = 0
           encontrados += 1

main()

Casi mágicamente, y muy rápido, obtenemos lo siguiente:

Encontré la solución [4, 6, 1, 5, 2, 0, 7, 3] en 328 intentos.
Encontré la solución [2, 5, 7, 1, 3, 0, 6, 4] en 820 intentos.
Encontré la solución [3, 1, 4, 7, 5, 0, 2, 6] en 488 intentos.
Encontré la solución [0, 6, 3, 5, 7, 1, 4, 2] en 262 intentos.
Encontré la solución [1, 7, 5, 0, 2, 4, 6, 3] en 264 intentos.
Encontré la solución [0, 6, 3, 5, 7, 1, 4, 2] en 181 intentos.
Encontré la solución [3, 7, 4, 2, 0, 6, 1, 5] en 2086 intentos.
Encontré la solución [3, 1, 6, 4, 0, 7, 5, 2] en 75 intentos.
Encontré la solución [5, 2, 0, 7, 4, 1, 3, 6] en 590 intentos.
Encontré la solución [5, 2, 0, 7, 3, 1, 6, 4] en 177 intentos.

Aquí hay un hecho interesante. Se sabe que en un tablero de 8x8 hay 92 soluciones diferentes del problema. Estamos tomando al azar una de las 40320 permutaciones posibles de nuestra representación. Así que nuestras chances de encontrar una solución en cada intento son de 92/40320. O dicho de otra forma, en promedio deberíamos necesitar 40320/92 intentos - unos 438.26 - antes de toparnos con una solución. Los 10 "números de intentos" que imprimimos coinciden bastante bien con nuestra teoría!

14.10) Glosario

• búsqueda binaria, lineal, búsqueda lineal, algoritmo de fusión (merge algorithm), prueba, desarrollo orientado a testeo (test-driven development, TDD)

14.11) Ejercicios

1) En la sección 14.7, Alicia en el País de las maravillas, otra vez! comenzamos con la observación de que el algoritmo de fusión (merge algorithm) aplica un patrón que puede ser reutilizado en otras situaciones. Adaptar el algoritmo de fusión para escribir cada una de las variantes que sugerimos allí: (hacerlo)

• a. Retornar sólo los elementos que están presentes en ambas listas.
• b. Retornar sólo los elementos que aparecen en la primera lista, pero no en la segunda.
• c. Retornar sólo los elementos que aparecen en la segunda lista, pero no en la primera.
• d. Retornar sólo elementos que están presentes o bien en la primera o bien en la segunda lista, pero no en ambas.
• e. Retornar elementos de la primera lista que no son eliminados por un elemento correspondiente en la segunda lista.
  
  • En este caso, un item en la segunda lista hace "knock out" a sólo un elemento de la primera lista que sea igual a él (no a todos los que sean iguales a él)
  • Esta operación a veces se llama bagdiff
  • Por ejemplo: bagdiff([5,7,11,11,11,12,13], [7,8,11]) retornaría [5, 11, 11, 12, 13]

2) Modificar el programa de las reinas para resolver tableros de tamaño 4, 12 y 16. ¿Cuál es el máximo tamaño de puzzle que puedes resolver habitualmente en menos de 1 minuto? (hacerlo)

3) Adaptar el programa de las reinas para que mantenga una lista de las soluciones que ya se imprimieron, para evitar así imprimir la misma solución más de una vez. (hacerlo)

4) Los tableros de ajedrez son simétricos. Si tenemos una solución para el problema de las reinas, su imagen especular - tanto si invertimos el tablero según el eje x como según el y - será también una solución. Y también si rotamos el tablero 90°, 180° o 270° tendremos una solución. En cierta forma, soluciones que son la imagen especular o la rotación de otras soluciones son menos interesantes que los "casos originales". De las 92 soluciones para el problema de las 8 reinas, sólo hay 12 familias únicas de soluciones, si se consideran las soluciones y se van descartando las imágenes especulares o rotaciones. Wikipedia tiene información muy interesante sobre el tema.

• a. Escribe una función que genere la imagen especular de una solución según el eje Y. (hacerlo)
• b. Escribe una función que genere la imagen especular de una solución según el eje Z. (hacerlo)
• c. Escribe una función que rote una solución 90° en sentido antihorario, y úsala para implementar una rotaciones de 180° y 270°. (hacerlo)
• d. Escribe una función que reciba una solución, y escriba la familia de simetrías para dicha solución. Por ejemplo, las simetrías de [0,4,7,5,2,6,1,3] son: (hacerlo)

[[0,4,7,5,2,6,1,3],[7,1,3,0,6,4,2,5],
 [4,6,1,5,2,0,3,7],[2,5,3,1,7,4,6,0],
 [3,1,6,2,5,7,4,0],[0,6,4,7,1,3,5,2],
 [7,3,0,2,5,1,6,4],[5,2,4,6,0,3,1,7]]

• e. Ahora adapta el programa de las reinas para que no liste soluciones que estén en la misma familia. Sólo imprime soluciones únicas de cada familia. (hacerlo)

5) Cada semana un programador compra 4 billetes de lotería. Siempre elige los mismos números primos, con la esperanza de que si llega a acertar, podrá ir a la TV y a Facebook y contarle a todo el mundo su secreto. Esto generará entonces un interés público generalizado en los números primos, y será el evento que dispare una nueva era de entusiasmo por las matemáticas. Representa sus billetes semanales en Python como una lista de listas:

mis_billetes = [ [ 7, 17, 37, 19, 23, 43],
               [ 7,  2, 13, 41, 31, 43],
               [ 2,  5,  7, 11, 13, 17],
               [13, 17, 37, 19, 23, 43] ]

Completa estos ejercicios: (hacerlo)

• a. Cada sorteo de lotería toma 6 bolas al azar, numeradas del 1 al 49. Escribe una función que retorne un sorteo de lotería.
• b. Escribe una función que compare un billete único y un sorteo, y retorne la cantidad de aciertos en el billete:

test(aciertos_billete([42,4,7,11,1,13], [2,5,7,11,13,17]) == 3)

• c. Escribe una función que reciba una lista de billetes y un sorteo, y retorne una lista indicando cuántos aciertos hubo en cada billete:

test(aciertos_billete([42,4,7,11,1,13], mis_billetes) == [1, 2, 3, 1])

• d. Escribe una función que tome una lista de enteros, y retorne la cantidad de números primos en la lista:

test(primos_en([42,4,7,11,1,13]) == 3)

• e. Escribe una función que revise si al programador le ha faltado algún número primo en su selección de 4 billetes. Devuelve una lista con todos los primos que le han faltado:

test(primos_faltantes(mis_billetes) == [3, 29, 47])

• f. Escribe una función que repetidamente genere un nuevo sorteo, y compare a éste con los 4 billetes.
  
  • i. Cuenta cuántos sorteos han sido necesarios antes de que al menos uno de los billetes tenga al menos 3 aciertos. Repite el experimento 20 veces, y toma el promedio de sorteos necesarios.
  • ii. ¿Cuántos sorteos son necesarios, en promedio, antes de que consiga al menos 4 aciertos con un billete?
  • iii. ¿Cuántos sorteos son necesarios, en promedio, antes de que consiga al menos 5 aciertos?
  • (Pista: esto puede llevar mucho tiempo - sería buena idea que imprimieras algunos puntos, como si fueran una barra de progreso, para señalar por ejemplo que se ha completado uno de los 20 experimentos)

• Observa que es difícil construir casos de testeo en este caso, porque nuestros números aleatorios no son determinísticos. El testeo automatizado sólo funciona realmente si sabes de antemano cuál debería ser la respuesta!

6) Lee Alicia en el País de las Maravillas. Puedes leerlo de la versión inglesa incluida aquí o de alguna versión gratuita online. Seguramente hay una versión disponible en la web de Project Gutenberg. Tienen versiones html y pdf, con imágenes, y miles de obras clásicas!