Parábola
Definición
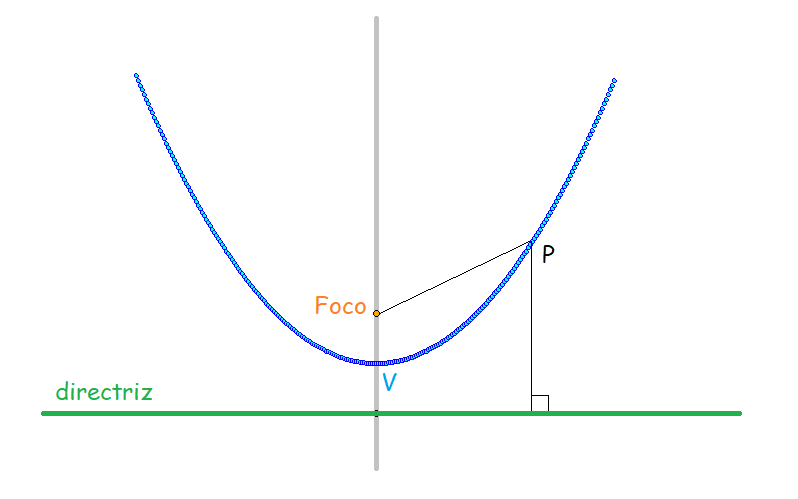
Lugar geométrico de los puntos del plano que equidistan de un punto F (Foco) y de una recta d (Directriz).
d(P, F) = d(P, d)
- Se llama Eje de la Parábola a la recta perpendicular a la directriz que pasa por el Foco.
- Se llama Vértice (V) al punto medio entre el Foco F y la intersección del eje con la directriz.
Parábola horizontal o vertical con vértice en el origen
Caso horizontal: Parábola de foco F (a, 0) y Vértice en V (0, 0):
y² = 4ax
x = y²/4a
- Ecuación de la directriz: x = -a
- Foco: F(a, 0)
Caso vertical: Parábola de foco F (0, a) y Vértice en V (0, 0):
x² = 4ay
y = x²/4a
- Ecuación de la directriz: y = -a
- Foco: F(0, a)
Parábola horizontal o vertical con vértice V (h, k)
Caso horizontal: El foco es F (h + a, k) y el Vértice V (h, k)
(y - k)² = 4a(x - h)
- Ecuación de la directriz: x = h - a
- Foco: F(h + a, k)
Caso vertical: El foco es F (h, k + a) y el vértice V (h, k)
(x - h)² = 4a(y - k)
- Ecuación de la directriz: y = k - a
- Foco: F(h, k + a)