Elipse
Definición
Lugar geométrico de los puntos del plano tales que la suma de sus distancias a dos puntos fijos (Focos F y F') es constante.
d(P, F) + d(P, F') = cte
a² = b² + c²
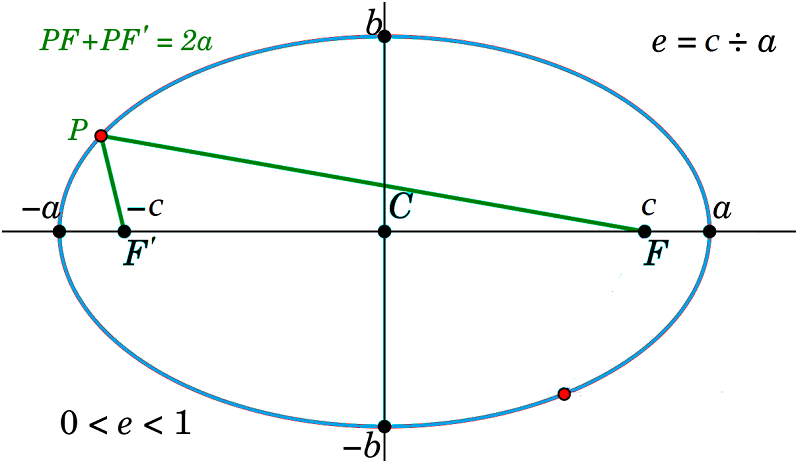
- Si P es un punto de la elipse, se cumple: FP + F'P = cte
- Focos: F y F'
- Vértices: A, A', B, B'
- Diámetro mayor: AA' = 2a
- Diámetro menor: BB' = 2b
- Distancias: OF = OF' = c
- OA = a
- OB = b
- Distancia Focal: FF' = 2c
Excentricidad
La excentricidad de una elipse es la razón entre su distancia focal y su eje mayor. Su valor se encuentra entre 0 y 1.
- Cuanto más baja, la elipse es más redondeada (más parecida a un círculo).
- Cuanto más alta, la elipse es más estirada (más parecida a un segmento).
e = c/a
- e = 0: Circunferencia
- e = 1: Segmento FF'
- 0 < e < 1 Elipse "normal"
Lado recto
(... lado recto ...)Elipse horizontal o vertical con centro en el origen
Caso horizontal: Elipse de centro O (0, 0) y focos F(c, 0) y F'(-c, 0)
x²/a² + y²/b² = 1
- Eje mayor: 2a (horizontal)
- Focos: F(c, 0) y F'(-c, 0)
- Recordar: b² = a² - c²
Caso vertical: Elipse de centro O (0, 0) y focos F(0, c) y F'(0, -c):
x²/b² + y²/a² = 1
- Eje mayor: 2a (vertical)
- Focos: F(0, c) y F'(0, -c)
- Recordar: b² = a² - c²
Elipse horizontal o vertical con centro C (h, k)
Caso horizontal: Centro C (h, k) y Focos F (h + c, k) y F' (h - c, k)
(x - h)²/a² + (y - k)²/b² = 1
- Eje mayor: 2a (horizontal)
- Focos: F(h + c, k) y F'(h - c, k)
- Recordar: b² = a² - c²
Caso vertical: Centro C (h, k) y Focos F (h, k + c) y F' (h, k - c)
(x - h)²/b² + (y - k)²/a² = 1
- Eje mayor: 2a (vertocal)
- Focos: F(h, k + c) y F'(h, k - c)
- Recordar: b² = a² - c²